Question

16．已知∠ABC与∠DEF的两边分别满足：BA∥ED，BC∥EF，若∠ABC=45°，则∠DEF的度数为45°或135°．

Answer 1

分析 分类讨论：如图①根据两直线平行，内错角相等由BA∥ED得∠ABC=∠1，由BC∥EF得∠1=∠DEF，然后利用等量代换得到∠ABC=∠DEF；如图②根据两直线平行，内错角相等由BA∥ED得∠ABC=∠1，再根据两直线平行，同旁内角互补由BC∥EF得∠1+∠DEF=180°，所以∠ABC+∠DEF=180°代入求出即可．

解答 解：如图①∵BA∥ED，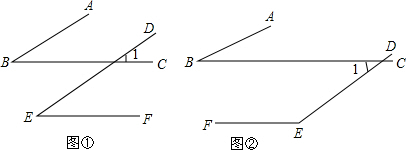
∴∠ABC=∠1，
∵BC∥EF，
∴∠1=∠DEF，
∴∠ABC=∠DEF，
∵∠ABC=45°，
∴∠DEF=45°；
如图②，∵BA∥ED，
∴∠ABC=∠1，
∵BC∥EF，
∴∠1+∠DEF=180°，
∴∠ABC+∠DEF=180°，
∵∠ABC=45°，
∴∠DEF=135°，
故答案为：45°或135°．

点评 本题考查了平行线的性质的应用，能求出符合条件的所有情况是解此题的关键，注意：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．