
����Ŀ����֪������y=a��x+3����x��1����a��0������x��������������ཻ��A��B���㣬��y���ཻ�ڵ�C��������A��ֱ��y=��![]() x+b�������ߵ���һ������ΪD��
x+b�������ߵ���һ������ΪD��
��1������D�ĺ�����Ϊ2���������ߵĺ�������ʽ��
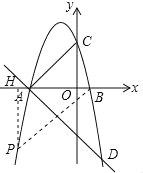
��2�����ڵ��������ڵ����������е�P��ʹ����A��B��PΪ��������������ABC���ƣ����P�����ꣻ
��3���ڣ�1���������£����E���߶�AD�ϵ�һ�㣨�����˵㣩������BE��һ����Q�ӵ�B���������߶�BE��ÿ��1����λ���ٶ��˶�����E�������߶�ED��ÿ��![]() ����λ���ٶ��˶�����D��ֹͣ���ʵ���E�������Ƕ���ʱ����Q�������˶�����������ʱ�����٣�
����λ���ٶ��˶�����D��ֹͣ���ʵ���E�������Ƕ���ʱ����Q�������˶�����������ʱ�����٣�
���𰸡�(1) y=��![]() x2��2
x2��2![]() x+3
x+3![]() ��(2) P����������4����
��(2) P������Ϊ����4����![]() ���ͣ���6����
���ͣ���6����![]() ����(3) ��1����4
����(3) ��1����4![]() ��.
��.
��������
�����������1�����ݶ��κ����Ľ���ʽȷ����A��B�����꣬���ֱ�ߵĽ���ʽ�������D�����꣬��������ߵĽ���ʽ����2����PH��x����H�����P������Ϊ��m��n�����֡�BPA�ס�ABC�͡�PBA�ס�ABC���������������ε����ʼ��㼴�ɣ���3����DM��x�ύ��������M����DN��x����N����EF��DM��F���������еĶ������Q���˶�ʱ��t=BE+EFʱ��t��С���ɣ�
�����������1����y=a��x+3����x��1����
���A����������3��0������B����������1��0����
��ֱ��y=��![]() x+b������A��
x+b������A��
��b=��3![]() ��
��
��y=��![]() x��3
x��3![]() ��
��
��x=2ʱ��y=��5![]() ��
��
���D��������2����5![]() ����
����
�ߵ�D���������ϣ�
��a��2+3����2��1��=��5![]() ��
��
��ã�a=��![]() ��
��
�������ߵĽ���ʽΪy=��![]() ��x+3����x��1��=��
��x+3����x��1��=��![]() x2��2
x2��2![]() x+3
x+3![]() ��
��
��2����PH��x����H��
���P��������m��n����
����BPA�ס�ABCʱ����BAC=��PBA��
��tan��BAC=tan��PBA����![]() =
=![]() ��
��
��![]() =
=![]() ����n=��a��m��1����
����n=��a��m��1����
��![]() ��
��
��ã�m1=��4��m2=1���������⣬��ȥ����
��m=��4ʱ��n=5a��
�ߡ�BPA�ס�ABC��
��![]() =
=![]() ����AB2=ACPB��
����AB2=ACPB��
��42=![]()
![]() ��
��
��ã�a1=![]() ���������⣬��ȥ����a2=��
���������⣬��ȥ����a2=��![]() ��
��
��n=5a=��![]() ��
��
���P����������4����![]() ����
����
����PBA�ס�ABCʱ����CBA=��PBA��
��tan��CBA=tan��PBA����![]() =
=![]() ��
��
��![]() =
=![]() ����n=��3a��m��1����
����n=��3a��m��1����
��![]() ��
��
��ã�m1=��6��m2=1���������⣬��ȥ����
��m=��6ʱ��n=21a��
�ߡ�PBA�ס�ABC��
��![]() =
=![]() ����AB2=BCPB��
����AB2=BCPB��
��42=![]()
![]() ��
��
��ã�a1=![]() ���������⣬��ȥ����a2=��
���������⣬��ȥ����a2=��![]() ��
��
���P����������6����![]() ����
����
�������������������ĵ�P������Ϊ����4����![]() ���ͣ���6����
���ͣ���6����![]() ����
����
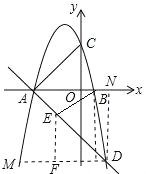
��3����DM��x�ύ��������M����DN��x����N����EF��DM��F��
��tan��DAN=![]() =
=![]() =
=
���DAN=60�㣬
���EDF=60�㣬
��DE=![]() =
=![]() EF��
EF��
��Q���˶�ʱ��t=![]() +
+![]() =BE+EF��
=BE+EF��
�൱BE��EF����ʱ��t��С��
��BE��DM��E(1,��4![]() )��
)��


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
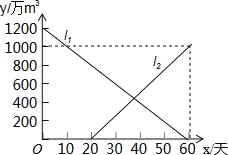
����Ŀ�����ڳ������º��������꣬ijˮ�����ˮ����ʱ������Ӷ����٣���֪ԭ����ˮ��y1����m3����ɺ�����ʱ��x���죩�Ĺ�ϵ��ͼ���߶�l1��ʾ��������ָɺ�������ӵ�20�쿪ʼ��ˮ��עˮ��עˮ��y2����m3����ʱ��x���죩�Ĺ�ϵ��ͼ���߶�l2��ʾ���������������أ���
��1����ԭ����ˮ��y1����m3����ʱ��x���죩�ĺ�����ϵʽ������x=20ʱ��ˮ������ˮ����
��2����0��x��60ʱ��ˮ�������ˮ��y����m3����ʱ��x���죩�ĺ�����ϵʽ��ע��x�ķ�Χ����������ˮ��������900��m3Ϊ���ظɺ���ֱ��д���������ظɺ�ʱx�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ȥ��������2ƿ����ΪmԪ�����Ϻ�3������ΪnԪ�����������_____Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017�������ڼ䣬����������7�������ÿ��Ӵ��ο͵�������ǰһ����ȵı仯�����������ʾ��ǰһ��������,������ʾ��ǰһ���ٵ����������±���
���� | 1�� | 2�� | 3�� | 4�� | 5�� | 6�� | 7�� |
�����仯/���� | +1.7 | +0.6 | +0.3 | -0.3 | -0.6 | +0.2 | -1.1 |
(1) ���ж��������ο���������������?���ٵ�������?��������������?
(2) ��9��30�յ��ο�����Ϊ3����,����7����ο��������Ƕ�������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ξ��ж�һ��ƽ���ı��β�һ�����е������ǣ� ��
A. �Խ������ B. �Խ���� C. �Խ�����ƽ�� D. �Ա����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����m��n�����в���ʽ��һ���������ǣ� ��
A. m+2��n+2 B. 2m��2n C. �� D. m2��n2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016ɽ��Ϋ����23��)���ι�˾�ھ�����������50���۹���ο�����ʹ�ã��ٶ�ÿ���۹һ�������ֻ�ܳ���һ�Σ���ÿ�����������x��Ԫ����5�ı���������ÿ���Ӫ�˹������£���x������100Ԫʱ���۹��ȫ���������x����100Ԫʱ��ÿ�����������ÿ����5Ԫ�����ȥ�Ĺ۹�ͻ����1������֪���й۹ÿ��Ĺ�������1100Ԫ��
��1���Żݻ�ڼ䣬Ϊʹ�۹ȫ�������ÿ��ľ�����Ϊ������ÿ���������������ӦΪ����Ԫ����ע��������=����멁�����ѣ�
��2����ÿ�����������Ϊ����Ԫʱ��ÿ��ľ�������ࣿ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com