
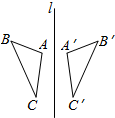
 如图,△ABC与△A′B′C′关于直线l对称,且∠A=98°,∠C′=48°,则∠B的度数为34°.
如图,△ABC与△A′B′C′关于直线l对称,且∠A=98°,∠C′=48°,则∠B的度数为34°. 科目:初中数学 来源: 题型:选择题
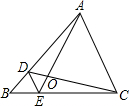 如图,D、E分别是△ABC边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则$\frac{DE}{AC}$的值为( )
如图,D、E分别是△ABC边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则$\frac{DE}{AC}$的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.请判断沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(精确到0.01)
中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.请判断沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(精确到0.01)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com