
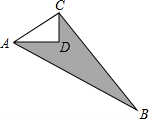
 如图,已知CD=3,AD=4,∠ADC=90°,BC=12,AB=13.则图中阴影部分的面积=24.
如图,已知CD=3,AD=4,∠ADC=90°,BC=12,AB=13.则图中阴影部分的面积=24. 分析 连接AC,利用勾股定理求出AC,求出△ABC是直角三角形,△ABC的面积减去△ACD的面积就是所求的面积.
解答 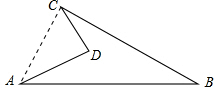 解:连结AC,
解:连结AC,
由勾股定理可知
AC=$\sqrt{C{D}^{2}+A{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
又∵AC2+BC2=52+122=132=AB2,
∴△ABC是直角三角形
故所求面积=S△ABC-S△ACD=$\frac{1}{2}$×5×12-$\frac{1}{2}$×3×4=30-6=24,
故答案为:24.
点评 此题主要考查了直角三角形面积公式以及勾股定理以及逆定理的应用.关键是掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
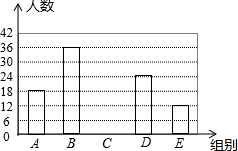 随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展,某旅游公司对我市一企业旅游年消费情况进行了问卷调查,随机抽取部分员工,记录每个人消费金额,并将调查数据适当调整,绘制成如图两幅尚不完整的表和图.
随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展,某旅游公司对我市一企业旅游年消费情况进行了问卷调查,随机抽取部分员工,记录每个人消费金额,并将调查数据适当调整,绘制成如图两幅尚不完整的表和图.| 组别 | 个人年消费金额x(元) | 频数(人数) | 频率 |
| A | x≤2000 | 18 | 0.15 |
| B | 2000<x≤4000 | a | b |
| C | 4000<x≤6000 | ||
| D | 6000<x≤8000 | 24 | 0.20 |
| E | x>8000 | 12 | 0.10 |
| 合计 | c | 1.00 | |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
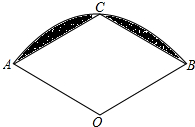 如图,在扇形AOB中,半径OA=2,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是$\frac{4π}{3}$-2$\sqrt{3}$(结果保留π).
如图,在扇形AOB中,半径OA=2,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是$\frac{4π}{3}$-2$\sqrt{3}$(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
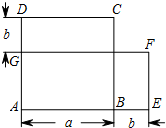 (1)如图,正方形ABCD的边长为a,周长为4a;长方形AEFG的长为a+b,宽为a-b,长为4a.
(1)如图,正方形ABCD的边长为a,周长为4a;长方形AEFG的长为a+b,宽为a-b,长为4a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com