
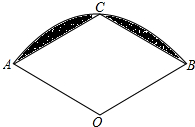
 如图,在扇形AOB中,半径OA=2,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是$\frac{4π}{3}$-2$\sqrt{3}$(结果保留π).
如图,在扇形AOB中,半径OA=2,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是$\frac{4π}{3}$-2$\sqrt{3}$(结果保留π). 分析 连接OC,过点A作AD⊥CD于点D,根据∠AOB=120°,C为弧AB的中点可知AC=BC,∠AOC=∠BOC=60°,故△ACO与△BOC为边长相等的两个等边三角形,再根据锐角三角函数的定义得出AD的长,由S阴影=S扇形AOB-2S△AOC即可得出结论.
解答 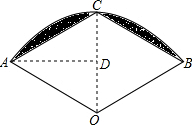 解:连接OC,过点A作AD⊥CD于点D,
解:连接OC,过点A作AD⊥CD于点D,
∵∠AOB=120°,C为弧AB的中点,
∴AC=BC,∠AOC=∠BOC=60°,
∴△ACO与△BOC为边长相等的两个等边三角形.
∵AO=2,
∴AD=OA•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
∴S阴影=S扇形AOB-2S△AOC=$\frac{120π×{2}^{2}}{360}$-2×$\frac{1}{2}$×2×$\sqrt{3}$=$\frac{4π}{3}$-2$\sqrt{3}$.
故答案为:$\frac{4π}{3}$-2$\sqrt{3}$.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
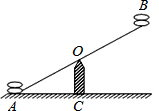 如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,当横板AB的A端着地时,测得∠OAC=α,则在玩跷跷板时,横板AB绕点O上下转动的最大角度为2α°.
如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,当横板AB的A端着地时,测得∠OAC=α,则在玩跷跷板时,横板AB绕点O上下转动的最大角度为2α°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
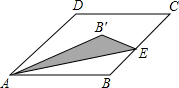 如图,已知在周长为20的菱形ABCD中,∠C=45°,点E是线段BC上一点,将△ABE沿AE所在直线翻折,使点B落在B′上,则在点E沿B→C→D运动的过程中,点B′运动的路径长是$\frac{5π}{4}$.
如图,已知在周长为20的菱形ABCD中,∠C=45°,点E是线段BC上一点,将△ABE沿AE所在直线翻折,使点B落在B′上,则在点E沿B→C→D运动的过程中,点B′运动的路径长是$\frac{5π}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com