
【题目】如图,表中给出的是某月的月历,任意选取“H”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现这7个数的和不可能的是()
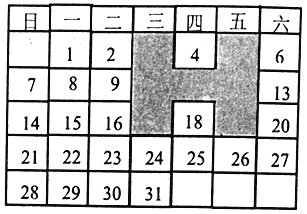
A.63B.70C.92D.105
 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于D,连结DC、DA、OA、OC,四边形OADC为平行四边形.
(1)求证:△BOC≌△CDA.
(2)若AB=2,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
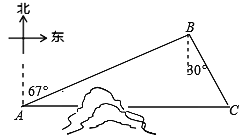
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,现计划开凿隧道使A、C两地直线贯通,经测量得:B地在A地的北偏东67°方向,距离A地280km,C地在B地南偏东的30°方向.
(1)求B地到直线AC的距离;
(2)求隧道开通后与隧道开通前相比,从A地到C地的路程将缩短多少?
(本题结果都精确到0.1km)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,E是AD的中点,过A点作BC的平行线交BE的延长线于F,连接CF.
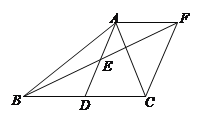

(1)线段AF与CD相等吗?为什么?
(2)如果AB=AC,试猜测四边形ADCF是怎样的特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你喜欢玩游戏吗?现请你玩一个转盘游戏.如图所示的两上转盘中指针落在每一个数字上的机会均等,现同时自由转动甲、乙两个转盘,转盘停止后,指针各指向一个数字,用所指的两个数字作乘积.所有可能得到的不同的积分别为_______________________;数字之积为奇数的概率为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(建立概念)如下图,A、B为数轴上不重合的两定点,点P也在该数轴上,我们比较线段![]() 和
和![]() 的长度,将较短线段的长度定义为点P到线段
的长度,将较短线段的长度定义为点P到线段![]() 的“靠近距离”.特别地,若线段
的“靠近距离”.特别地,若线段![]() 和
和![]() 的长度相等,则将线段
的长度相等,则将线段![]() 或
或![]() 的长度定义为点P到线段
的长度定义为点P到线段![]() 的“靠近距离”.
的“靠近距离”.
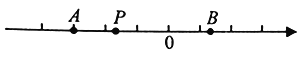
(概念理解)如下图,数轴的原点为O,点A表示的数为![]() ,点B表示的数为4.
,点B表示的数为4.
(1)点O到线段![]() 的“靠近距离”为________;
的“靠近距离”为________;
(2)点P表示的数为m,若点P到线段![]() 的“靠近距离”为3,则m的值为_________;
的“靠近距离”为3,则m的值为_________;

(拓展应用)(3)如下图,在数轴上,点P表示的数为![]() ,点A表示的数为
,点A表示的数为![]() ,点B表示的数为6. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动.设移动的时间为
,点B表示的数为6. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动.设移动的时间为![]() 秒,当点P到线段
秒,当点P到线段![]() 的“靠近距离”为3时,求t的值.
的“靠近距离”为3时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梯形ABCD中AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向形外作等腰直角三角形,其面积分别是![]() ,且
,且![]() ,则CD=( )
,则CD=( )

A.2.5ABB.3ABC.3.5ABD.4AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在直线AB上,OC⊥AB .在RtΔODE中,∠ODE=90°,∠DOE=30°,先将ΔODE一边OE与OC重合(如图1),然后将ΔODE绕点O按顺时针方向旋转(如图2),当OE与OC 重合时停止旋转.
(1)当∠AOD=80°时,则旋转角∠COE的大小为____________ ;
(2)当OD在OC与OB之间时,求∠AOD![]() ∠COE的值;
∠COE的值;
(3)在ΔODE的旋转过程中,若∠AOE=4∠COD时,求旋转角∠COE的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com