
【题目】如图,在△ABC中,D是BC的中点,E是AD的中点,过A点作BC的平行线交BE的延长线于F,连接CF.
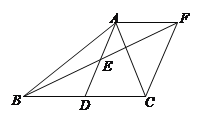

(1)线段AF与CD相等吗?为什么?
(2)如果AB=AC,试猜测四边形ADCF是怎样的特殊四边形,并说明理由.
【答案】(1)相等;(2)矩形
【解析】
试题(1)由E是AD的中点可得AE=DE,由AF∥BC可得∠EBD=∠EFA,∠EDB=∠EAF,即可证得△AEF≌△DEB,从而得到结果;
(2)由AF∥CD ,AF=CD可得四边形ADCF为平行四边形,由AB=AC,D是BC的中点根据等腰三角形的性质可得∠ADC=90°,从而得到结果.
(1)∵E是AD的中点
∴AE=DE
∵AF∥BC
∴∠EBD=∠EFA,∠EDB=∠EAF
∴△AEF≌△DEB
∴AF=BD
∵BD=CD
∴AF=CD;
(2)四边形ADCF为矩形
∵AF∥CD,AF=CD
∴四边形ADCF为平行四边形
∵AB=AC,D是BC的中点
∴∠ADC=90°
∴四边形ADCF为矩形.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
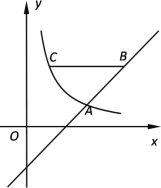
【题目】如图,在直角坐标系![]() 中,反比例函数图像与直线
中,反比例函数图像与直线![]() 相交于横坐标为3的点A.
相交于横坐标为3的点A.
(1)求反比例函数的解析式;
(2)如果点B在直线![]() 上,点C在反比例函数图像上,BC//
上,点C在反比例函数图像上,BC//![]() 轴,BC= 4,且BC在点A上方,求点B的坐标.
轴,BC= 4,且BC在点A上方,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八(3)班全体同学参加植树苗活动,下面是今年3月份该班同学植树苗情况的扇形统计图和不完整的条形统计图:
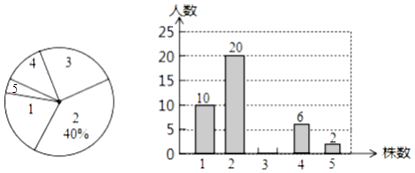
请根据以上统计图中的信息解答下列问题.
(1)该班同学共________人,植树苗3株的人数为________人;
(2)该班同学植树苗株数的中位数是________;
(3)小明用以下方法计算该班同学平均植树苗的株数是:![]() (株),根据你所学知识判断小明的计算是否正确,若不正确,请计算出正确的结果.
(株),根据你所学知识判断小明的计算是否正确,若不正确,请计算出正确的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)求证:抛物线与![]() 轴必定有公共点;
轴必定有公共点;
(2)若P(![]() ,y1),Q(-2,y2)是抛物线上的两点,且y1
,y1),Q(-2,y2)是抛物线上的两点,且y1![]() y2,求
y2,求![]() 的取值范围;
的取值范围;
(3)设抛物线与x轴交于点![]() 、
、![]() ,点A在点B的左侧,与y轴负半轴交于点C,且
,点A在点B的左侧,与y轴负半轴交于点C,且![]() ,若点D是直线BC下方抛物线上一点,连接AD交BC于点E,记△ACE的面积为S1,△DCE的面积为S2,求
,若点D是直线BC下方抛物线上一点,连接AD交BC于点E,记△ACE的面积为S1,△DCE的面积为S2,求![]() 是否有最值?若有,求出该最值;若没有,请说明理由.
是否有最值?若有,求出该最值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的普及,某手机厂商采用先网络预定,然后根据订单量生产手机的方式销售,2015年该厂商将推出一款新手机,根据相关统计数据预测,定价为2200元,日预订量为20000台,若定价每减少100元,则日预订量增加10000台.
(1)设定价减少x元,预订量为y台,写出y与x的函数关系式;
(2)若每台手机的成本是1200元,求所获的利润w(元)与x(元)的函数关系式,并说明当定价为多少时所获利润最大;
(3)若手机加工厂每天最多加工50000台,且每批手机会有5%的故障率,通过计算说明每天最多接受的预订量为多少?按最大量接受预订时,每台售价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,在正方形 ABCD 中,对角线 AC, BD 交于点 O ,点 E 在 AB 上,点 F 在 BC 的延长线上,且 AE CF .连接 EF 交 AC 于点 P, 分别连接 DE, DF .
(1)求证: ADE CDF ;
(2)求证: PE PF ;
(3)如图 2,若 PE BE, 则![]() 的值是 .(直接写出结果即可).
的值是 .(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,表中给出的是某月的月历,任意选取“H”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现这7个数的和不可能的是()
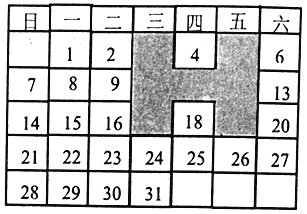
A.63B.70C.92D.105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等。四位同学各自发表了下述见解:
甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形;
乙:只要指针连续转六次,一定会有一次停在6号扇形;
丙:指针停在奇数号扇形的概率与停在偶数号扇形的概率相等;
丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大。

其中,你认为正确的见解有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若![]() 和
和![]() 是同类项,则m=_____,n=_________。
是同类项,则m=_____,n=_________。
(2)单项式![]() 的系数是_______,次数是_______。
的系数是_______,次数是_______。
(3)多项式![]() 是_______次_______项式,其中第二项的系数是________。
是_______次_______项式,其中第二项的系数是________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com