
【题目】已知抛物线![]() .
.
(1)求证:抛物线与![]() 轴必定有公共点;
轴必定有公共点;
(2)若P(![]() ,y1),Q(-2,y2)是抛物线上的两点,且y1
,y1),Q(-2,y2)是抛物线上的两点,且y1![]() y2,求
y2,求![]() 的取值范围;
的取值范围;
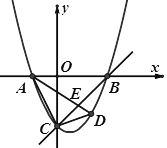
(3)设抛物线与x轴交于点![]() 、
、![]() ,点A在点B的左侧,与y轴负半轴交于点C,且
,点A在点B的左侧,与y轴负半轴交于点C,且![]() ,若点D是直线BC下方抛物线上一点,连接AD交BC于点E,记△ACE的面积为S1,△DCE的面积为S2,求
,若点D是直线BC下方抛物线上一点,连接AD交BC于点E,记△ACE的面积为S1,△DCE的面积为S2,求![]() 是否有最值?若有,求出该最值;若没有,请说明理由.
是否有最值?若有,求出该最值;若没有,请说明理由.
【答案】(1)见解析;(2)![]() 或
或![]() ,(3)
,(3)![]() 没有最小值;
没有最小值;![]() 有最大值是
有最大值是![]()
【解析】分析:(1)本题需先根据判别式解出无论m为任何实数都大于零,再判断出物线与x轴总有交点.
(2)分两种情况:当点P在对称轴的左侧时,![]() 随
随![]() 的增大而减小,得
的增大而减小,得![]() ;当点P在对称轴的右侧时,
;当点P在对称轴的右侧时,![]() 随
随![]() 的增大而增大,
的增大而增大,![]() ,故得解.
,故得解.
详解:(1)令![]() 得
得![]()
∴![]()
∴![]()
无论![]() 取何值,
取何值,![]()
∴ 抛物线与![]() 轴必定有公共点
轴必定有公共点
(2)∵![]() ,抛物线的对称轴是
,抛物线的对称轴是![]()
当点P在对称轴的左侧时,![]() 随
随![]() 的增大而减小,
的增大而减小,
∵y1![]() y2,
y2, ![]()
当点P在对称轴的右侧时,![]() 随
随![]() 的增大而增大,
的增大而增大,
Q(-2,y2)关于对称轴的对称点是(3,y2)
∵y1![]() y2,
y2, ![]()
综上所述:![]() 或
或![]()
(3)![]() ,
,![]()
∵![]() 、∴
、∴ ![]() ,解得
,解得![]() 或
或![]()
∴ ![]()
∴ ![]() 、
、![]() ,
,![]()
∴ 直线BC的解析式是![]()
设点A到直线BC的距离是![]() ,点D到直线BC的距离是
,点D到直线BC的距离是![]() ,
,
△ACE的面积S1![]() ,△DCE的面积S2
,△DCE的面积S2![]()
∴ ![]() ,
,![]()
∴ 求![]() 的最值转化为求
的最值转化为求![]() 的最值
的最值
设过点D与直线BC平行的直线解析式为![]()
当点D在直线BC下方的抛物线上运动时,![]() 无最小值,仅当直线
无最小值,仅当直线![]() 与抛物线
与抛物线![]() 只有一个公共点时,
只有一个公共点时,![]() 有最大值
有最大值
即方程组![]() 有两个相等的实数根
有两个相等的实数根
∴![]() ,
, ![]() ,
,
∴![]() ,此时
,此时![]()
∴ ![]() 没有最小值;
没有最小值;![]() 有最大值是
有最大值是![]()
∴![]() 、
、![]()


科目:初中数学 来源: 题型:
【题目】如图,某公司计划用32m长的材料沿墙建造的长方形仓库,仓库的一边靠墙,已知墙长16m,设长方形的宽AB为xm.

(1)用x的代数式表示长方形的长BC;
(2)能否建造成面积为120㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由;
(3)能否建造成面积为160㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点A,B,D,C,其中AB=2,BD=3,DC=1,如图所示,设点A,B,D,C所对应数的和是p.
(1)①若以B为原点.写出点A,D,C所对应的数,并计算p的值;
②若以D为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=x,p=﹣71,求x.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的不完整统计表,根据表中信息,回答下列问题:
喜爱的电视节目类型 | 人数 | 频率 |
新闻 | 4 | 0.08 |
体育 | / | / |
动画 | 15 | / |
娱乐 | 18 | 0.36 |
戏曲 | / | 0.06 |
(1)本次共调查了_______名学生,若将各类电视节目喜爱的人数所占比例绘制成扇形统计图,则“喜爱动画”对应扇形的圆心角度数是_______;
(2)该校共有2000名学生,根据调查结果估计该校“喜爱体育”节目的学生人数;
(3)在此次问卷调查中,甲、乙两班分别有![]() 人喜爱新闻节目,若从这
人喜爱新闻节目,若从这![]() 人中随机抽取
人中随机抽取![]() 人去参加“新闻小记者”培训,求抽取的
人去参加“新闻小记者”培训,求抽取的![]() 人来自不同班级的概率.
人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
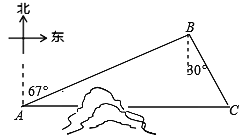
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,现计划开凿隧道使A、C两地直线贯通,经测量得:B地在A地的北偏东67°方向,距离A地280km,C地在B地南偏东的30°方向.
(1)求B地到直线AC的距离;
(2)求隧道开通后与隧道开通前相比,从A地到C地的路程将缩短多少?
(本题结果都精确到0.1km)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,且
,且![]() 、
、![]() 、
、![]() 分别是点A. B. C在数轴上对应的数.
分别是点A. B. C在数轴上对应的数.

(1)写出![]() =___;
=___;![]() =___;
=___;![]() =___.
=___.
(2)若甲、乙、丙三个动点分别从A.B.C三点同时出发沿数轴负方向运动,它们的速度分别是1、2、4,(单位/秒),运行![]() 秒后,甲、乙、丙三个动点对应的位置分别为:
秒后,甲、乙、丙三个动点对应的位置分别为:![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求式子
时,求式子![]() 的值.
的值.
(3)若甲、乙、丙三个动点分别从A,B,C三点同时出发沿数轴正方向运动,它们的速度分别是1,2,4(单位/秒),运动多长时间后,乙与甲、丙等距离?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,E是AD的中点,过A点作BC的平行线交BE的延长线于F,连接CF.
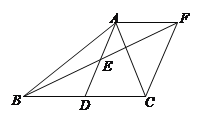

(1)线段AF与CD相等吗?为什么?
(2)如果AB=AC,试猜测四边形ADCF是怎样的特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(建立概念)如下图,A、B为数轴上不重合的两定点,点P也在该数轴上,我们比较线段![]() 和
和![]() 的长度,将较短线段的长度定义为点P到线段
的长度,将较短线段的长度定义为点P到线段![]() 的“靠近距离”.特别地,若线段
的“靠近距离”.特别地,若线段![]() 和
和![]() 的长度相等,则将线段
的长度相等,则将线段![]() 或
或![]() 的长度定义为点P到线段
的长度定义为点P到线段![]() 的“靠近距离”.
的“靠近距离”.
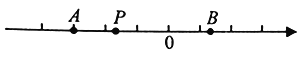
(概念理解)如下图,数轴的原点为O,点A表示的数为![]() ,点B表示的数为4.
,点B表示的数为4.
(1)点O到线段![]() 的“靠近距离”为________;
的“靠近距离”为________;
(2)点P表示的数为m,若点P到线段![]() 的“靠近距离”为3,则m的值为_________;
的“靠近距离”为3,则m的值为_________;

(拓展应用)(3)如下图,在数轴上,点P表示的数为![]() ,点A表示的数为
,点A表示的数为![]() ,点B表示的数为6. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动.设移动的时间为
,点B表示的数为6. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动.设移动的时间为![]() 秒,当点P到线段
秒,当点P到线段![]() 的“靠近距离”为3时,求t的值.
的“靠近距离”为3时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,将一副直角三角板按如图所示的方式摆放,其中三角形ABC为含60°角的直角三角板,三角形BDE为含45°角的直角三角板.

(1)如图1,若点D在AB上,则∠EBC的度数为 ;
(2)如图2,若∠EBC=170°,则∠α的度数为 ;
(3)如图3,若∠EBC=118°,求∠α的度数;
(4)如图3,若0°<∠α<60°,求∠ABE-∠DBC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com