
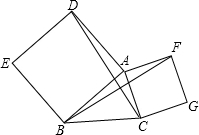
 以△ABC的AB、AC为边分别作正方形ADEB、ACGF,连接DC、BF.
以△ABC的AB、AC为边分别作正方形ADEB、ACGF,连接DC、BF. (1)证明:∵四边形ABED和四边形ACGF都是正方形
(1)证明:∵四边形ABED和四边形ACGF都是正方形
|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| AB |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、y=-x2+2 |
| B、y=-x2+1 |
| C、y=-( x-2)2+1 |
| D、y=-( x+2)2+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠C=90°,AC=BC=m,延长CA到D,使AD=AB,连接BD.
如图,在Rt△ABC中,∠C=90°,AC=BC=m,延长CA到D,使AD=AB,连接BD.| (cos45°-tan22.5°)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
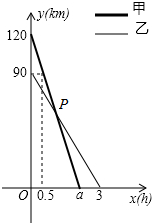 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图,请回答下列问题:
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图,请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com