
 如图,在Rt△ABC中,∠C=90°,AC=BC=m,延长CA到D,使AD=AB,连接BD.
如图,在Rt△ABC中,∠C=90°,AC=BC=m,延长CA到D,使AD=AB,连接BD.| (cos45°-tan22.5°)2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| BC |
| CD |
| m | ||
(
|
| 2 |
| 2 |
| (cos45°-tan22.5°)2 |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| BC |
| CD |


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
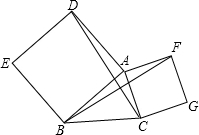 以△ABC的AB、AC为边分别作正方形ADEB、ACGF,连接DC、BF.
以△ABC的AB、AC为边分别作正方形ADEB、ACGF,连接DC、BF.查看答案和解析>>
科目:初中数学 来源: 题型:
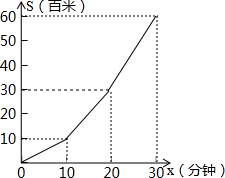 小明利用星期六、日双休骑自行车到城外小姨家去玩,星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家,行程情况如图所示.星期日小明又沿原路返回自己家中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是( )
小明利用星期六、日双休骑自行车到城外小姨家去玩,星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家,行程情况如图所示.星期日小明又沿原路返回自己家中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是( )| A、30分钟 | ||
B、38
| ||
C、41
| ||
D、43
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com