
【题目】解下列方程
(1)![]() (2)
(2)![]()
【答案】(1) x1=1;(2) x1=-1,x2=3,x3=-2,x4=4.
【解析】
(1)方程去分母转化为整式方程,求出整式方程的解,经检验即可得到分式方程的解;
(2)运用换元法求解即可.
(1)方程两边同乘以(x+2)(x-2),得
(x-2)+4x-2(x+2)=(x+2)(x-2),
即x2-3x+2=0,
∴x1=1,x2=2.
检验:x=1时,(x+2)(x-2)≠0,知x=1是原方程的解;x=2时,(x+2)(x-2)=0,知x=2是原方程的增根. 故原方程的根是x=1.
(2)设x2-2x=y,
则原方程变形为![]()
(y+2)(y+1)+25(y-2)(y+1)=24(y2-4)
整理后,得y2-11y+24=0.
解得 y1=3,y2=8.
①当y=3时,x2-2x=3,
解得 x1=-1,x2=3,
②当y=8时,x2-2x=8.
解得x3=-2,x4=4.
经检验:x1=-1,x2=3,x3=-2,x4=4都是原方程的解.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,小明和小颖对一道应用题进行了合作探究:一列火车匀速行驶,经过一条长为1000米的隧道需要50秒,整列火车完全在隧道里的时间是30秒,求火车的长度.
(1)请补全小明的探究过程:设火车的长度为x米,则从车头进入隧道到车尾离开隧道所走的路程为(1000+x)米,所以这段时间内火车的平均速度为![]() 米/秒;由题意,火车的平均速度还可以表示为 米/秒.再根据火车的平均速度不变,可列方程 ,解方程后可得火车的长度为 米.
米/秒;由题意,火车的平均速度还可以表示为 米/秒.再根据火车的平均速度不变,可列方程 ,解方程后可得火车的长度为 米.
(2)小颖认为:也可以通过设火车的平均速度为v米/秒,列出方程解决问题.请按小颖的思路完成探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
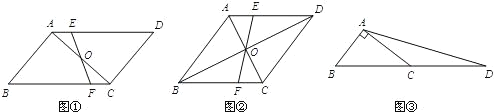
【题目】(1)猜想:如图①,在![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,过点
的中点,过点![]() 的直线分别交
的直线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,若
,若![]() 的面积是8,则四边形
的面积是8,则四边形![]() 的面积是________.
的面积是________.
(2)探究:如图②,在菱形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,过点
,过点![]() 的直线分别交
的直线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
(3)应用:如图③,在![]() 中,
中,![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的面积是_______.
的面积是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某起重机厂四月份生产A型起重机25台,B型起重机若干台.从五月份起, A型起重机月增长率相同,B型起重机每月增加3台.已知五月份生产的A型起重机是B型起重机的2倍,六月份A、 B型起重机共生产54台.求四月份生产B型起重机的台数和从五月份起A型起重机的月增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把以下各数分别填入相应的集合里.3.14、0.121121112…、(﹣1![]() )2、|﹣6|、﹣2011、﹣22、
)2、|﹣6|、﹣2011、﹣22、![]() π、0、20%
π、0、20%
无理数集合:{ …}
负整数集合:{ …}
分数集合:{ …}
正数集合:{ …}
查看答案和解析>>
科目:初中数学 来源: 题型:
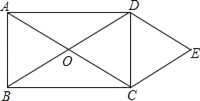
【题目】如图所示,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=3,BC=4,求四边形OCED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是矩形ABCD的边AB、BC的中点,连AF,CE,AF、CE交于G,则四边形BEGF与四边形ADCG的面积的比值为___________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com