练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，E、F分别是矩形ABCD的边AB、BC的中点，连AF，CE，AF、CE交于G，则四边形BEGF与四边形ADCG的面积的比值为___________.

    【答案】1:4

    【解析】过点G作AB、BC的垂线，连接BG，AC，

    S矩形ABCD=ABBC，

    S△BCE=ABBC，S△ABF=ABBC，

    S△AEG=S△GCF，即AEGN=CFGM，

    S四边形GEBF=S△BEG+S△BFG=BEGN+BFGM=2S△AEG=2S△GCF，

    ∴S△BCE=3S△GCF=ABBC，

    ∴S四边形GEBF=2S△GCF=ABBC，

    S四边形ADCG=S矩形ABCD-S△AEG-S△BCE=ABBC-ABBC-ABBC=ABBC，

    ∴S四边形GEBF：S四边形ADCG=1：4，

    故答案为：1：4.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】解下列方程

    （1）　 （2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了提高科技创新意识，我市某中学在“2018年科技节”活动中举行科技比赛，包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类别的比赛)，根据各类别参赛人数制成不完全的条形统计图和扇形统计图如下：

    请根据以上图品信息，解答下列问题：

    (1)全体参赛的学生共有_______人，扇形统计图中“建模”所在扇形的圆心角是_______°；

    (2)将条形统计图补充完整；

    (3)在比赛结果中，获得“环保”类一等奖的学生为1名男生和2名女生，获得“建模”类一等奖的学生为1名男生和1名女生．现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动．则选取的两人中恰为1名男生1名女生的概率是______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算

    （1）1﹣12+4

    （2）﹣7﹣（﹣5）2÷（﹣1）2

    （3）

    （4）

    （5）（用科学记数法表示）8.56×102﹣2.1×103

    （6）用简便方法计算：﹣99×48

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某检修小组从地出发，在东西向的马路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中七次行驶纪录如下．（单位：）

    第一次

    第二次

    第三次

    第四次

    第五次

    第六次

    第七次

    （1）在第__________次记录时距地最远；

    （2）求收工时距地多远？

    （3）若每千米耗油升，每升汽油需元，问检修小组工作一天需汽油费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

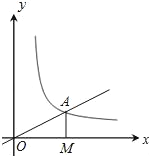
    【题目】如图，正比例函数y=x的图象与反比例函数y=（k≠0）在第一象限的图象交于A点，过A点作x轴的垂线AM，垂足为M，已知△OAM的面积为1．

    （1）求反比例函数的解析式；

    （2）求点A的坐标；

    （3）如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上确定一点P，使PA+PB最小．求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

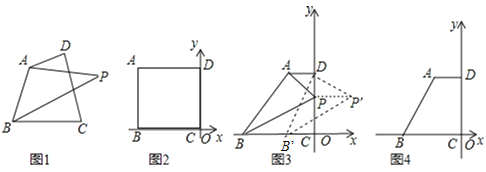
    【题目】如图1，点P为四边形ABCD所在平面上的点，如果∠PAD=∠PBC，则称点P为四边形ABCD关于A、B的等角点，以点C为坐标原点，BC所在直线为轴建立平面直角坐标系，点B的横坐标为﹣6．

    （1）如图2，若A、D两点的坐标分别为A（﹣6，4）、D（0，4），点P在DC边上，且点P为四边形ABCD关于A、B的等角点，则点P的坐标为　_________　；

    （2）如图3，若A、D两点的坐标分别为A（﹣2，4）、D（0，4）．

    ①若P在DC边上时，则四边形ABCD关于A、B的等角点P的坐标为　_________　；

    ②在①的条件下，将PB沿轴向右平移个单位长度（0＜＜6）得到线段P′B′，连接P′D，B′D，试用含的式子表示P′D2+B′D2，并求出使P′D2+B′D2取得最小值时点P′的坐标；

    ③如图4，若点P为四边形ABCD关于A、B的等角点，且点P坐标为（1， ），求的值；

    ④以四边形ABCD的一边为边画四边形，所画的四边形与四边形ABCD有公共部分，若在所画的四边形内存在一点P，使点P分别是各相邻两顶点的等角点，且四对等角都相等，请直接写出所有满足条件的点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

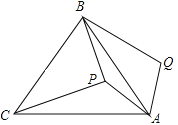
    【题目】（2016四川省达州市）如图，P是等边三角形ABC内一点，将线段AP绕点A顺时针旋转60°得到线段AQ，连接BQ．若PA=6，PB=8，PC=10，则四边形APBQ的面积为____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知数轴上，点O为原点，点A对应的数为9，点B对应的数为b，点C在点B右侧，长度为2个单位的线段BC在数轴上移动．

    （1）当b＝5时，试求线段AC的长；

    （2）当线段BC在数轴上沿射线AO方向移动的过程中，若存在AC﹣OB＝AB，求此时满足条件的b值．

    （3）当线段BC在数轴上移动时，满足关系式|AC﹣OB|＝|AB﹣OC|，则此时的b的取值范围是　 　．

    查看答案和解析>>

    同步练习册答案