
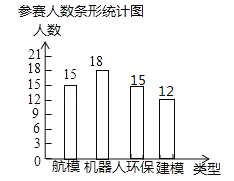
����Ŀ��Ϊ����߿Ƽ�������ʶ������ij��ѧ����2018��Ƽ�������о��пƼ���������������ģ������������������������������ģ���ĸ����(ÿ��ѧ��ֻ�ܲμ�һ�����ı���)�����ݸ������������Ƴɲ���ȫ������ͳ��ͼ������ͳ��ͼ���£�
���������ͼƷ��Ϣ������������⣺


(1)ȫ�������ѧ������_______�ˣ�����ͳ��ͼ������ģ���������ε�Բ�Ľ���_______����
(2)������ͳ��ͼ����������
(3)�ڱ�������У��������������һ�Ƚ���ѧ��Ϊ1��������2��Ů�����������ģ����һ�Ƚ���ѧ��Ϊ1��������1��Ů�����ִ���������һ�Ƚ���ѧ���и����ѡȡ1��ѧ���μ��м���������ģ����������ѡȡ��������ǡΪ1������1��Ů���ĸ�����______.
���𰸡� 60 72 ![]()
����������������1��������ģ������������ռ�ٷֱȿɵ���������������ģ����ռ�ٷֱȳ���360���ɵ����ӦԲ�ĽǶ�����
��2������������������������ٷֱȿɵ�������������������ȥ�����������͵������ɵ�����ģ�����������ɲ�ȫ����ͼ��
��3���������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����ѡȡ��������ǡΪ1����1Ů��������������ø��ʹ�ʽ������ô𰸣�
�������1��ȫ�������ѧ������15��25%=60���ˣ�������ģ��������ͳ��ͼ�е�Բ�Ľ��ǣ�1��25%��30%��25%����360��=72�㣻
�ʴ�Ϊ����1��60��72��
��2����������������Ϊ��60��25%=15���ˣ�������ģ��������Ϊ��60��15��18��15=12���ˣ�����ȫ����ͼ��ͼ��
��3������״ͼ��ͼ��
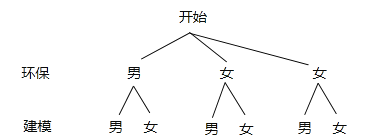
�߹���6�ֵȿ��ܽ��������������ǡΪ1����1Ů������3�ֽ������ѡȡ��������ǡΪ1����1Ů���ĸ������� ![]() =
=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ���ϣ�С����Сӱ��һ��Ӧ��������˺���̽����һ�л�������ʻ������һ����Ϊ1000��������Ҫ50�룬���л���ȫ���������ʱ����30�룬��ij��ȣ�
��1���벹ȫС����̽�����̣���ij���Ϊx�ף���ӳ�ͷ������������β�뿪�������ߵ�·��Ϊ��1000+x���ף��������ʱ���ڻ�ƽ���ٶ�Ϊ![]() ��/�룻�����⣬��ƽ���ٶȻ����Ա�ʾΪ�� ����/�룮�ٸ��ݻ�ƽ���ٶȲ��䣬���з����� �����ⷽ�̺�ɵûij���Ϊ�� ���ף�
��/�룻�����⣬��ƽ���ٶȻ����Ա�ʾΪ�� ����/�룮�ٸ��ݻ�ƽ���ٶȲ��䣬���з����� �����ⷽ�̺�ɵûij���Ϊ�� ���ף�
��2��Сӱ��Ϊ��Ҳ����ͨ�����ƽ���ٶ�Ϊv��/�룬�г����̽�����⣮�밴Сӱ��˼·���̽�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
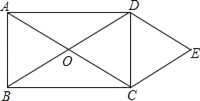
����Ŀ����ͼ��ʾ��OΪ����ABCD�Խ��ߵĽ��㣬DE��AC��CE��BD��
��1�����ж��ı���OCED����״����˵�����ɣ�
��2����AB��3��BC��4�����ı���OCED���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
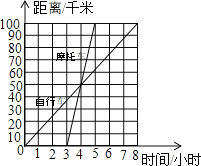
����Ŀ����ͼ����ʾһ�����г�����һ��Ħ�г�������ͬ·���ɼص��ҵ���ʻ���̵�ͼ�����ؼ�ľ�����100ǧ�ף������ͼ��ش�������������.
��1��˭�����Ľ��磿��ʱ�䣿˭�����ҵ��磿�絽�ʱ�䣿
��2��������;����ʻ���ٶȷֱ��Ƕ��٣�
��3��ָ����ʲôʱ�������������ʻ��;�У������ʱ���ڣ�
�����г���ʻ��Ħ�г�ǰ�棻
�����г���Ħ�г�������
�����г���ʻ��Ħ�г����棿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
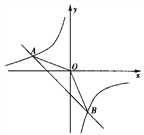
����Ŀ����ͼ��һ�κ���![]() ��ͼ���뷴����
��ͼ���뷴����![]() ��ͼ���ཻ��A��-2��1����B��
��ͼ���ཻ��A��-2��1����B��![]() ��-2������.
��-2������.
(1)����������һ�κ����Ľ���ʽ��
(2) ����ABO�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У�AC��BC����DΪAB�е㣮��GDH��90�㣬��GDH�Ƶ�D��ת��DG��DH�ֱ����AC��BC����E��F���㣮���н��ۣ���AE+BF��AC����AE2+BF2��EF2����S�ı���CEDF��![]() S��ABC������DEFʼ��Ϊ����ֱ�������Σ�������ȷ����(����)
S��ABC������DEFʼ��Ϊ����ֱ�������Σ�������ȷ����(����)

A. �٢ڢۢ� B. �٢ڢ� C. �٢� D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E��F�ֱ��Ǿ���ABCD�ı�AB��BC���е㣬��AF��CE��AF��CE����G�����ı���BEGF���ı���ADCG������ı�ֵΪ___________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�����ǰ尴��ͼ��ʾ�ķ�ʽ���ã������н����в���ȷ����( )

A. ��1����3 B. �����2��30��������AC��DE
C. �����2��30��������BC��AD D. �����2��30��������4����C
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com