
【题目】数学课上,小明和小颖对一道应用题进行了合作探究:一列火车匀速行驶,经过一条长为1000米的隧道需要50秒,整列火车完全在隧道里的时间是30秒,求火车的长度.
(1)请补全小明的探究过程:设火车的长度为x米,则从车头进入隧道到车尾离开隧道所走的路程为(1000+x)米,所以这段时间内火车的平均速度为![]() 米/秒;由题意,火车的平均速度还可以表示为 米/秒.再根据火车的平均速度不变,可列方程 ,解方程后可得火车的长度为 米.
米/秒;由题意,火车的平均速度还可以表示为 米/秒.再根据火车的平均速度不变,可列方程 ,解方程后可得火车的长度为 米.
(2)小颖认为:也可以通过设火车的平均速度为v米/秒,列出方程解决问题.请按小颖的思路完成探究过程.
科目:初中数学 来源: 题型:
【题目】填空:在横线上填写适当的式,数或符号,完整表达解方程的过程
解方程:![]() ,
,
解:两边平方,得_____________________________________________
整理,得_____________________________________________________
解这个方程得, ![]() ___________________,
___________________,![]() _____________________
_____________________
检验:把![]() ________分别带入原方程两边,左边=_______________,右边=_________________,由右边__________左边,可知
________分别带入原方程两边,左边=_______________,右边=_________________,由右边__________左边,可知![]() ________是________
________是________
把x=_________________分别带入原方程两边,左边=________,左边=_________________右边,可知![]() ________是________
________是________
所以,原方程的根是___________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某水文站在雨季对某条河一周内水位变化情况的记录(上升为正,下降为负)
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
水位变化/ | +0.2 | +0.3 | -0.4 | -0.4 | -0.1 | +0.2 | +0.4 |
注:①表中记录的数据为每天中午12时的水位与前一天12时水位的变化量;②上星期日12时的水位高度为![]() .
.

(1)请你通过计算说明本周日与上周日相比,水位是上升了还是下降了;
(2)用折线连接本周每天的水位,并根据折线说明水位在本周内的升降趋势.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的长为6,宽为4,将长方形先向上平移2个单位,再向右平移2个单位得到长方形![]() ,则阴影部分面积是( )
,则阴影部分面积是( )
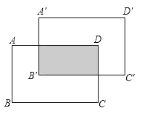
A.12B.10C.8D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,延长AB至点E,延长CD至点F,使得
中,延长AB至点E,延长CD至点F,使得![]() ,连接EF,分别交AD,BC于点M,N,连接AN,CM.
,连接EF,分别交AD,BC于点M,N,连接AN,CM.
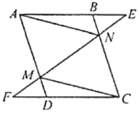
(1)求证:![]() ;
;
(2)四边形AMCN是平行四边形吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区某陶瓷厂计划一周生产陶瓷工艺品350个,平均每天生产50个,但实际每天生产量与计划相比有出入,下表是某周的生产情况(以50个为标准,超产记为正、减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减(单位:个) | +4 | -6 | -7 | +15 | -5 | +16 | -8 |
(1)根据记录的数据,请直接写出该厂本周产量最多的一天比最少的一天多生产的工艺品的个数;
(2)该工艺厂在本周实际生产工艺品的数量为多少个?(列式计算);
(3)已知该厂实行每周计件工资制,每周结算一次,每生产一个工艺品可得6元,若超额完成任务(以350个为标准),则超过部分每个另奖12元,少生产每个扣4元,试求该陶瓷厂在这一周应付出的工资总额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高科技创新意识,我市某中学在“2018年科技节”活动中举行科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类别的比赛),根据各类别参赛人数制成不完全的条形统计图和扇形统计图如下:
请根据以上图品信息,解答下列问题:


(1)全体参赛的学生共有_______人,扇形统计图中“建模”所在扇形的圆心角是_______°;
(2)将条形统计图补充完整;
(3)在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类一等奖的学生为1名男生和1名女生.现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动.则选取的两人中恰为1名男生1名女生的概率是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com