
【题目】如图在平面直角坐标系中,![]() ,
,![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,则点
,则点![]() 的坐标为___________.
的坐标为___________.

【答案】![]() 或
或![]()
【解析】
当点C在AB上方时,过点C作CE⊥y轴于点E,易证△AOB≌△BEC(AAS),根据全等三角形的性质可得BE=AO=4,EC=OB=2,从而得到点C的坐标为(2,6),同理可得当点C在AB下方时,点C的坐标为:(-2,-2).
解:如图所示,当点C在AB上方时,过点C作CE⊥y轴于点E,
∵![]() ,
,![]() ,四边形
,四边形![]() 为正方形,
为正方形,
∴∠BEC=∠AOB=90°,BC=AB,
∵∠BCE+∠EBC=90°,∠OBA+∠EBC=90°,
∴∠BCE=∠OBA,
∴△AOB≌△BEC(AAS),
∴BE=AO=4,EC=OB=2,
∴OE=OB+BE=6,
∴此时点C的坐标为:(2,6),
同理可得当点C在AB下方时,点C的坐标为:(-2,-2),
综上所述,点C的坐标为:![]() 或
或![]()
故答案为:![]() 或
或![]() .
.



 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
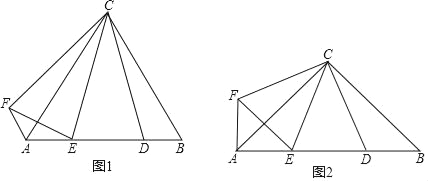
【题目】(1)操究发现:如图1,△ABC为等边三角形,点D为AB边上的一点,∠DCE=30°,∠DCF=60°且CF=CD
①求∠EAF的度数;
②DE与EF相等吗?请说明理由
(2)类比探究:如图2,△ABC为等腰直角三角形,∠ACB=90°,点D为AB边上的一点,∠DCE=45°,CF=CD,CF⊥CD,请直接写出下列结果:
①∠EAF的度数
②线段AE,ED,DB之间的数量关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径,AD=12,点B、C在⊙O上,AB、DC的延长线交于点E,且CB=CE,∠BCE=70°.

有以下结论:①∠ADE=∠E;②劣弧![]() 的长为
的长为![]() ;③点C为
;③点C为![]() 的中点;④BD平分∠ADE.以上结论一定正确的是_________________.(把正确结论的序号都填上)
的中点;④BD平分∠ADE.以上结论一定正确的是_________________.(把正确结论的序号都填上)
【答案】①②③
【解析】分析:①根据内接四边形的对角互补得到∠CBE=∠ADE,根据等腰三角形的性质得到∠CBE=∠E,即可证明.
②求出圆心角的度数,根据弧长公式求解即可.
③证明∠DAC=∠EAC,即可证明.
④∠A≠∠E,BD不平分∠ADE.
详解:①∠CBE为圆内接四边形ABCD的外角,则∠CBE=∠ADE,
CB=CE,所以∠CBE=∠E,因此∠ADE=∠E.
②∠A=∠BCE=70°,∴∠AOB=40°,![]() 的长=
的长=![]()
③由题意知:AC⊥DE,由∠ADE=∠E得AD=AE,
∴∠DAC=∠EAC,∴点C为![]() 的中点.
的中点.
④DB⊥AE,而∠A≠∠E,∴BD不平分∠ADE. 正确结论①②③
故答案为:①②③.
点睛:属于圆的综合题,考查圆内接四边形的性质,圆周角定理,弧长公式等,考查知识点较多,对学生综合分析能力要求较高.
【题型】填空题
【结束】
15
【题目】计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意四个有理数![]() 、
、![]() 、
、![]() 、
、![]() ,可以组成两个有理数对
,可以组成两个有理数对![]() 与
与![]() .我们规定:
.我们规定:
![]()
![]()
![]() .
.
例如:![]()
![]()
![]() .
.
根据上述规定解决下列问题:
(1)有理数对![]()
![]()
![]() ______;
______;
(2)若有理数对![]()
![]()
![]() ,求
,求![]() 的值;
的值;
(3)当满足等式![]()
![]()
![]() 的
的![]() 是整数时,求整数
是整数时,求整数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,小明和小颖对一道应用题进行了合作探究:一列火车匀速行驶,经过一条长为1000米的隧道需要50秒,整列火车完全在隧道里的时间是30秒,求火车的长度.
(1)请补全小明的探究过程:设火车的长度为x米,则从车头进入隧道到车尾离开隧道所走的路程为(1000+x)米,所以这段时间内火车的平均速度为![]() 米/秒;由题意,火车的平均速度还可以表示为 米/秒.再根据火车的平均速度不变,可列方程 ,解方程后可得火车的长度为 米.
米/秒;由题意,火车的平均速度还可以表示为 米/秒.再根据火车的平均速度不变,可列方程 ,解方程后可得火车的长度为 米.
(2)小颖认为:也可以通过设火车的平均速度为v米/秒,列出方程解决问题.请按小颖的思路完成探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
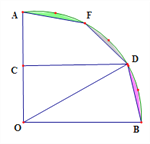
【题目】如图,扇形纸片AOB中,已知∠AOB=90,OA=6,取OA的中点C,过点C作DC⊥OA交![]() 于点D,点F是
于点D,点F是![]() 上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD、DF、FA依次剪下,则剩下的纸片(阴影部分)面积是______________.
上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD、DF、FA依次剪下,则剩下的纸片(阴影部分)面积是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
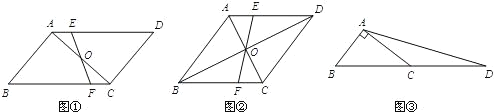
【题目】(1)猜想:如图①,在![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,过点
的中点,过点![]() 的直线分别交
的直线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,若
,若![]() 的面积是8,则四边形
的面积是8,则四边形![]() 的面积是________.
的面积是________.
(2)探究:如图②,在菱形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,过点
,过点![]() 的直线分别交
的直线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
(3)应用:如图③,在![]() 中,
中,![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的面积是_______.
的面积是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把以下各数分别填入相应的集合里.3.14、0.121121112…、(﹣1![]() )2、|﹣6|、﹣2011、﹣22、
)2、|﹣6|、﹣2011、﹣22、![]() π、0、20%
π、0、20%
无理数集合:{ …}
负整数集合:{ …}
分数集合:{ …}
正数集合:{ …}
查看答案和解析>>
科目:初中数学 来源: 题型:
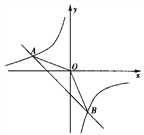
【题目】如图,一次函数![]() 的图象与反比例
的图象与反比例![]() 的图象相交于A(-2,1),B(
的图象相交于A(-2,1),B(![]() ,-2)两点.
,-2)两点.
(1)求反比例函数和一次函数的解析式;
(2) 求△ABO的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com