
����Ŀ����ͼ��AD����O��ֱ����AD=12����B��C����O�ϣ�AB��DC���ӳ��߽��ڵ�E����CB=CE����BCE=70��.

�����½��ۣ��١�ADE=��E�����ӻ�![]() �ij�Ϊ
�ij�Ϊ![]() ���۵�CΪ
���۵�CΪ![]() ���е㣻��BDƽ�֡�ADE.���Ͻ���һ����ȷ����_________________.������ȷ���۵���Ŷ����ϣ�
���е㣻��BDƽ�֡�ADE.���Ͻ���һ����ȷ����_________________.������ȷ���۵���Ŷ����ϣ�
���𰸡��٢ڢ�
���������������ٸ����ڽ��ı��εĶԽǻ����õ���CBE=��ADE�����ݵ��������ε����ʵõ���CBE=��E������֤��.
�����Բ�ĽǵĶ��������ݻ�����ʽ��⼴��.
��֤����DAC=��EAC������֤��.
�ܡ�A����E��BD��ƽ�֡�ADE.
��⣺�١�CBEΪԲ�ڽ��ı���ABCD����ǣ����CBE=��ADE��
CB=CE�����ԡ�CBE=��E����ˡ�ADE=��E.
�ڡ�A=��BCE=70�㣬���AOB=40�㣬![]() �ij�=
�ij�=![]()
��������֪��AC��DE���ɡ�ADE=��E��AD=AE��
���DAC=��EAC�����CΪ![]() ���е�.
���е�.
��DB��AE������A����E����BD��ƽ�֡�ADE. ��ȷ���ۢ٢ڢ�
�ʴ�Ϊ���٢ڢ�.
�㾦������Բ���ۺ��⣬����Բ�ڽ��ı��ε����ʣ�Բ�ܽǶ�����������ʽ�ȣ�����֪ʶ��϶࣬��ѧ���ۺϷ�������Ҫ��ϸ�.
�����͡������
��������
15
����Ŀ�����㣺![]() .
.

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪƽ���ı��Σ���BAD�Ľ�ƽ����AE��CD�ڵ�F����BC���ӳ����ڵ�E��
��1����֤��BE=CD��
��2������BF����BF��AE����BEA=60�㣬AB=4����ƽ���ı���ABCD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90������ACΪֱ������O����AB��D������O��OE��AB����BC��E��
��1����֤��EDΪ��O�����ߣ�
��2�������O�İ뾶Ϊ![]() ��ED=2���ӳ�EO����O��F������DF��AF������ADF�������
��ED=2���ӳ�EO����O��F������DF��AF������ADF�������

���𰸡���1��֤������������2��![]()
�������������������1����������OD����OE��AB������ƽ��������������ε����ʣ���֤��![]() ��
��![]() ���ɵ�
���ɵ�![]() �����֤��
�����֤��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�
��2������CD������ֱ�����Ե�Բ�ܽ���ֱ�ǣ����ɵ�![]() ���ù��ɶ����������
���ù��ɶ����������![]() �ij�������OE��AB��֤��
�ij�������OE��AB��֤��![]() �������������εĶ�Ӧ�߳ɱ������������
�������������εĶ�Ӧ�߳ɱ������������![]() �ij���Ȼ���������Ǻ�����֪ʶ�����
�ij���Ȼ���������Ǻ�����֪ʶ�����![]() ��
��![]() �ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
�ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
���������(1)֤��������OD��

��OE��AB��
���COE=��CAD����EOD=��ODA��
��OA=OD,
���OAD=��ODA��
���COE=��DOE��
�ڡ�COE�͡�DOE�У�
 ���COE�ա�DOE(SAS)��
���COE�ա�DOE(SAS)��
![]()
��ED��OD��
��ED��![]() �����ߣ�
�����ߣ�
(2)����CD����OE��M��
��Rt��ODE��
��OD=32��DE=2��
![]()
��OE��AB��
���COE�ס�CAB��
![]() ��AB=5��
��AB=5��
��AC��ֱ����
![]()
![]()
![]()
![]()
��EF��AB��
![]()
![]()
![]()
��S��ADF=S����ABEFS����DBEF
![]()
���ADF�����Ϊ![]()

�����͡������
��������
25
����Ŀ������Ŀ����֪��������y=ax2+ax+b��a��0����ֱ��y=2x+m��һ��������M��1��0������a��b��
��1����b��a�Ĺ�ϵʽ�������ߵĶ���D���꣨��a�Ĵ���ʽ��ʾ����
��2��ֱ���������ߵ�����һ�������ΪN������DMN�������a�Ĺ�ϵʽ��
��3��a=��1ʱ��ֱ��y=��2x���������ڵڶ������ڵ�G����G��H����ԭ��Գƣ��ֽ��߶�GH��y������ƽ��t����λ��t��0�������߶�GH����������������ͬ�Ĺ����㣬����t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ��![]() ��
��![]() ���ҳ��з��������е��������ĵ�����ͬ���������Ҳ��ͬ�����������������֮����
���ҳ��з��������е��������ĵ�����ͬ���������Ҳ��ͬ�����������������֮����![]() Ԫ�����������ĵ��۱�����ĵ��۵�
Ԫ�����������ĵ��۱�����ĵ��۵�![]() ����
����![]() Ԫ��
Ԫ��
��1�����ͬѧ���е�������������ĵ��۸��Ƕ���Ԫ��
��2��ijһ���ͬѧ�Ͻ֣�ǡ�ø����̼Ҵ���������![]() ������Ʒ����������ۣ�����
������Ʒ����������ۣ�����![]() ȫ������ÿ��
ȫ������ÿ��![]() Ԫ������ȯ
Ԫ������ȯ![]() Ԫ���ۣ�����
Ԫ���ۣ�����![]() Ԫ����ȯ������ȯȫ��ͨ�ã�������ֻ����
Ԫ����ȯ������ȯȫ��ͨ�ã�������ֻ����![]() ԪǮ�������ֻ��һ�ҳ��й����е���������Ʒ������˵��������ѡ����һ�ҹ����������Ҷ�����ѡ������һ�ҹ����ʡǮ��
ԪǮ�������ֻ��һ�ҳ��й����е���������Ʒ������˵��������ѡ����һ�ҹ����������Ҷ�����ѡ������һ�ҹ����ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±���ijˮ��վ���꼾��ij����һ����ˮλ�仯����ļ�¼������Ϊ�����½�Ϊ����
ʱ�� | ����һ | ���ڶ� | ������ | ������ | ������ | ������ | ������ |
ˮλ�仯/ | +0.2 | +0.3 | -0.4 | -0.4 | -0.1 | +0.2 | +0.4 |
ע���ٱ��м�¼������Ϊÿ������12ʱ��ˮλ��ǰһ��12ʱˮλ�ı仯��������������12ʱ��ˮλ�߶�Ϊ![]() .
.

��1������ͨ������˵������������������ȣ�ˮλ�������˻����½��ˣ�
��2�����������ӱ���ÿ���ˮλ������������˵��ˮλ�ڱ����ڵ���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC�У���ACB��90�㣬CD��AB��D����BAC��ƽ���߷ֱ�BC��CD��E��F��
��1����˵����CEF�ǵ��������Σ�
��2������Eǡ�����߶�AB�Ĵ�ֱƽ�����ϣ���˵���߶�AC���߶�AB֮���������ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ij�Ϊ6����Ϊ4����������������ƽ��2����λ��������ƽ��2����λ�õ�������![]() ������Ӱ���������( )
������Ӱ���������( )
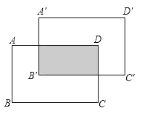
A.12B.10C.8D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�![]() ��
��![]() ����
����![]() ����������
����������![]() �����
�����![]() ������Ϊ___________.
������Ϊ___________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������˵������ֱ����һ��ƽ�ǣ�������߶�AB��BC����B���߶�AC���е㣻������AB������BA��ʾͬһ���ߣ�����һ������2���ķŴ�ȥ��һ���ǣ����������2����������֮�䣬ֱ����̣���120.5�㣽120��30�䣬������ȷ���У�������
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com