
【题目】如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( )
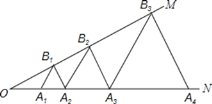
A. 64B. 32C. 16D. 8
【答案】A
【解析】
根据等边三角形的性质以及平行线的判定得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2=16…进而得出答案.
解:如图:
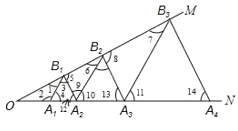
∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°120°30°=30°,
又∵∠3=60°,
∴∠5=180°60°30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,

∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
以此类推:A7B7=64B1A2=64.
故选:A


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
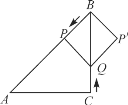
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=10cm,点P从点B出发,沿BA方向以每秒![]() cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1 cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,当四边形QPBP′为菱形时,t的值为____.
cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1 cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,当四边形QPBP′为菱形时,t的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,一次函数y=(1-3k)x+2k-1,试回答:
(1)k为何值时,y随x的增大而减小?
(2)k为何值时,图像与y轴交点在x轴上方?
(3) 若一次函数y=(1-3k)x+2k-1经过点(3,4).请求出一次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】城区某新建住宅小区计划购买并种植甲、乙两种树苗共300株.已知甲种树苗每株60元,乙种树苗每株90元.
(1)若购买树苗共用21000元,问甲、乙两种树苗应各买多少株?
(2)据统计,甲、乙两种树苗每株树苗对空气的净化指数分别为![]() 和
和![]() ,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:有两条边相等的三角形叫做等腰三角形。类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
(1)请你写出一个等对边四边形的名称;
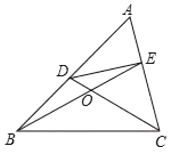
(2)如图,在△ABC中,点D、E分别在AB、AC上,设CD、BE相交于点O,若∠A=50°,![]() .请写出图中其余等于50°的角,并猜想图中哪个四边形为等对边四边形(不需证明);
.请写出图中其余等于50°的角,并猜想图中哪个四边形为等对边四边形(不需证明);
(3)在![]() 中,如果∠A是不等于50°的锐角,点D、E分别在AB、AC上,且
中,如果∠A是不等于50°的锐角,点D、E分别在AB、AC上,且![]() .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.学生借阅图书的次数统计表
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息,解答下列问题:
![]() ______,
______,![]() ______.
______.
![]() 该调查统计数据的中位数是______,众数是______.
该调查统计数据的中位数是______,众数是______.
![]() 请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
![]() 若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
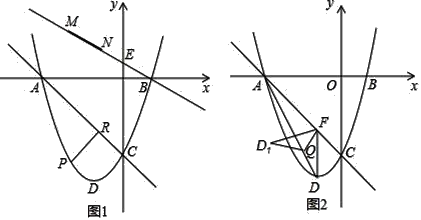
【题目】如图1,已知抛物线y=x2+2x﹣3与x轴相交于A,B两点,与y轴交于点C,D为顶点.
(1)求直线AC的解析式和顶点D的坐标;
(2)已知E(0, ![]() ),点P是直线AC下方的抛物线上一动点,作PR⊥AC于点R,当PR最大时,有一条长为
),点P是直线AC下方的抛物线上一动点,作PR⊥AC于点R,当PR最大时,有一条长为![]() 的线段MN(点M在点N的左侧)在直线BE上移动,首尾顺次连接A、M、N、P构成四边形AMNP,请求出四边形AMNP的周长最小时点N的坐标;
的线段MN(点M在点N的左侧)在直线BE上移动,首尾顺次连接A、M、N、P构成四边形AMNP,请求出四边形AMNP的周长最小时点N的坐标;
(3)如图2,过点D作DF∥y轴交直线AC于点F,连接AD,Q点是线段AD上一动点,将△DFQ沿直线FQ折叠至△D1FQ,是否存在点Q使得△D1FQ与△AFQ重叠部分的图形是直角三角形?若存在,请求出AQ的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
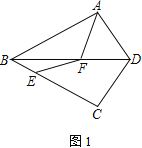
【题目】如图,△ABD、△CBD关于直线BD对称,点E是BC上一点,线段CE的垂直平分线交BD于点F,连接AF、EF.
(1) 求证:AF=EF;
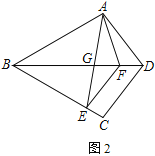
(2) 如图2,连接AE交BD于点G.若EF∥CD,求证:![]() ;
;
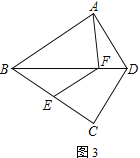
(3) 如图3,若∠BAD=90°,且点E在BF的垂直平分线上,tan∠ABD=![]() ,DF=
,DF=![]() ,请直接写出AF的长.
,请直接写出AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com