
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2).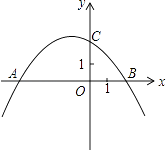
(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A、C、D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;
(3)以AB为直径作⊙M,直线经过点E(﹣1,﹣5),并且与⊙M相切,求该直线的解析式.
【答案】
(1)解:如图1,
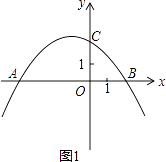
由题可得:
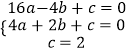 ,
,
解得: 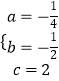 ,
,
∴抛物线的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+2;
x+2;
(2)解:过点D作DH⊥AB于H,交直线AC于点G,如图2.
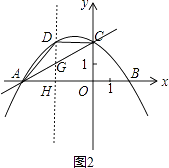
设直线AC的解析式为y=kx+t,
则有 ![]() ,
,
解得: ![]() ,
,
∴直线AC的解析式为y= ![]() x+2.
x+2.
设点D的横坐标为m,则点G的横坐标也为m,
∴DH=﹣ ![]() m2﹣
m2﹣ ![]() m+2,GH=
m+2,GH= ![]() m+2,
m+2,
∴DG=﹣ ![]() m2﹣
m2﹣ ![]() m+2﹣
m+2﹣ ![]() m﹣2=﹣
m﹣2=﹣ ![]() m2﹣m,
m2﹣m,
∴S△ADC=S△ADG+S△CDG
= ![]() DGAH+
DGAH+ ![]() DGOH=
DGOH= ![]() DGAO=2DG
DGAO=2DG
=﹣ ![]() m2﹣2m=﹣
m2﹣2m=﹣ ![]() (m2+4m)
(m2+4m)
=﹣ ![]() (m2+4m+4﹣4)
(m2+4m+4﹣4)
=﹣ ![]() [(m+2)2﹣4]
[(m+2)2﹣4]
=﹣ ![]() (m+2)2+2.
(m+2)2+2.
∴当m=﹣2时,S△ADC取到最大值2.
此时yD=﹣ ![]() ×(﹣2)2﹣
×(﹣2)2﹣ ![]() ×(﹣2)+2=2,
×(﹣2)+2=2,
即点D的坐标为(﹣2,2);
(3)解:设过点E的直线与⊙M相切于点F,与x轴交于点N,连接MF,如图3,
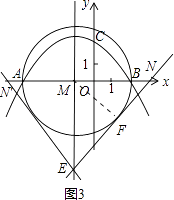
则有MF⊥EN.
∵A(﹣4,0),B(2,0),
∴AB=6,MF=MB=MA=3,
∴点M的坐标为(﹣4+3,0)即M(﹣1,0).
∵E(﹣1,﹣5),∴ME=5,∠EMN=90°.
在Rt△MFE中,EF= ![]() =
= ![]() =4.
=4.
∵∠MEF=∠NEM,∠MFE=∠EMN=90°,
∴△MEF∽△NEM,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴NM= ![]() ,
,
∴点N的坐标为(﹣1+ ![]() ,0)即(
,0)即( ![]() ,0)或(﹣1﹣
,0)或(﹣1﹣ ![]() ,0)即(﹣
,0)即(﹣ ![]() ,0).
,0).
设直线EN的解析式为y=px+q.
①当点N的坐标为( ![]() ,0)时,
,0)时,
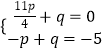 ,
,
解得: 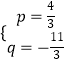 ,
,
∴直线EN的解析式为y= ![]() x﹣
x﹣ ![]() .
.
②当点N的坐标为(﹣ ![]() ,0)时,
,0)时,
同理可得:直线EN的解析式为y=﹣ ![]() x﹣
x﹣ ![]() .
.
综上所述:所求直线的解析式为y= ![]() x﹣
x﹣ ![]() 或y=﹣
或y=﹣ ![]() x﹣
x﹣ ![]() .
.
【解析】(1)将已知三点的坐标代入抛物线的解析式可得到关于a、b、c的方程组,从而可求得a、b、c的值;
(2)过点D作DH⊥AB,垂足为H,交直线AC于点G,然后再求得AC的解析式,设点D的横坐标为m,则点G的横坐标也为m,从而可以用m的代数式表示出DG,然后用割补法得到△ADC的面积是关于m的二次函数,最后依据二次函数的最值即可;
(3)设过点E的直线与⊙M相切于点F,与x轴交于点N,连接MF,由切线的性质可知:MF⊥EN.然后再求得点M的坐标以及线段ME、MF、EF的长,接下来,再证明△MEF∽△NEM,然后依据相似三角形的性质可求出MN的长度,从而得到点N的坐标,最后,再运用待定系数法求解即可.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=30°,BC=2 ![]() ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )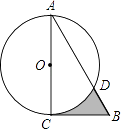
A.![]() ﹣
﹣ ![]()
B.![]() ﹣
﹣ ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某鞋店销售了9双鞋,各种尺码的销售量如下:
鞋的尺码 | 20 | 21 | 22 | 23 |
销售量(双) | 1 | 2 | 4 | 2 |
(1)计算这9双鞋尺码的平均数、中位数和众数.
(2)哪一个指标是鞋厂最感兴趣的指标?哪一个指标是鞋厂最不感兴趣的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,AF∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.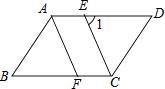
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF都是等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.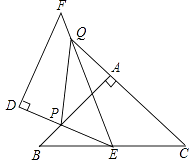
(1)求证:△BPE∽△CEQ;
(2)求证:DP平分∠BPQ;
(3)当BP=a,CQ= ![]() a,求PQ长(用含a的代数式表示).
a,求PQ长(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学的1号教学大楼共有4道门,其中两道正门大小相同,两道侧门也大小相同,安全检查时,对4道门进行了测试,当同时开启一道正门和两道侧门时,2分钟内可以通过560名学生,当同时开启一道正门和一道侧门时,4分钟内可通过800名学生.
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)该中学的2号教学大楼,有和1号教学大楼相同的正门和侧门共5道,若这栋大楼的教室里最多有1920名学生,安全检查规定,在紧急情况下,全大楼学生应在4分钟内通过这5道门安全撤离,该栋大楼正门和侧门各有几道?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
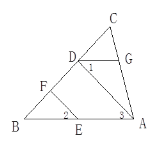
解: 因为EF∥AD,
所以∠2=____ (_________________________________)
又因为∠1=∠2
所以∠1=∠3 (__________________)
所以AB∥_____ (___________________________________)
所以∠BAC+______=180°(___________________________)
因为∠BAC=70°
所以∠AGD=_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com