
【题目】如图,在Rt△ABC中,∠A=30°,BC=2 ![]() ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )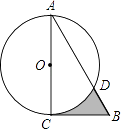
A.![]() ﹣
﹣ ![]()
B.![]() ﹣
﹣ ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
【答案】A
【解析】解:如图连接OD、CD. 
∵AC是直径,
∴∠ADC=90°,
∵∠A=30°,
∴∠ACD=90°﹣∠A=60°,
∵OC=OD,
∴△OCD是等边三角形,
∵BC是切线.
∴∠ACB=90°,∵BC=2 ![]() ,
,
∴AB=4 ![]() ,AC=6,
,AC=6,
∴S阴=S△ABC﹣S△ACD﹣(S扇形OCD﹣S△OCD)
= ![]() ×6×2
×6×2 ![]() ﹣
﹣ ![]() ×3×
×3× ![]() ﹣(
﹣( ![]() ﹣
﹣ ![]() ×32)
×32)
= ![]() ﹣
﹣ ![]() π.
π.
所以答案是:A.
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题:
(1)图1中“统计与概率”所在扇形的圆心角为度;
(2)图2、3中的a= , b=;
(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国人口增长速度的减慢,小学入学儿童数量有所减少.下表中的数据近似地呈现了某地区入学儿童人数的变化趋势:

(1)上表中_____是自变量,_____是因变量.
(2)你预计该地区从_____年起入学儿童的人数不超过1 000人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子中装有四张完全相同的卡片,分别写着2cm,3cm,4cm和5cm,盒子外有两张卡片,分别写着3cm和5cm,现随机从盒中取出一张卡片,与盒子外的两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,那么这三条线段能构成三角形的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为直线
为直线![]() 上一动点(不与点
上一动点(不与点![]() 重合),在
重合),在![]() 的右侧作
的右侧作![]() ,使得
,使得![]() ,
,![]() ,连接
,连接![]() .
.
(1)当点![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() ;
;
(2)当![]() 时,若点
时,若点![]() 在线段
在线段![]() 上,
上,![]() 中最小角为
中最小角为![]() ,请求出
,请求出![]() 的度数;
的度数;
(3)在点![]() 的运动过程中,当
的运动过程中,当![]() 垂直于
垂直于![]() 的某边时,求
的某边时,求![]() 的度数(用含
的度数(用含![]() 的代数式表示).
的代数式表示).
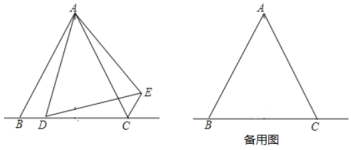
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2).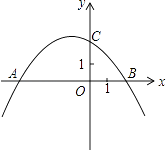
(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A、C、D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;
(3)以AB为直径作⊙M,直线经过点E(﹣1,﹣5),并且与⊙M相切,求该直线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com