
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() 是角平分线,
是角平分线,![]() 是高,
是高,![]() 和
和![]() 交于点
交于点![]() .
.
(1)若![]() ,则
,则![]() ____________
____________![]() ,
,![]() ____________
____________![]() ;
;
(2)结合(1)中的结果,探究![]() 和
和![]() 的关系,并说明理由.
的关系,并说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,见解析.
,见解析.
【解析】
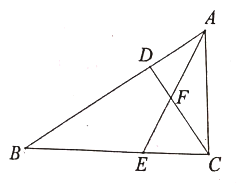
(1)根据∠ACD+∠BAC=∠B+∠BAC=90°,可得∠ACD=∠B,再根据AE是角平分线,可得∠BAE=∠CAF,再根据∠CFE是△ACF的外角,∠CEF是△ABE的外角,即可得到∠CFE和∠CEF的度数;
(2)根据∠ACD+∠BAC=∠B+∠BAC=90°,可得∠ACD=∠B,再根据AE是角平分线,可得∠BAE=∠CAF,再根据∠CFE是△ACF的外角,∠CEF是△ABE的外角,即可得到∠CFE=CAF+∠ACD,∠CEF=∠B+∠BAE,进而得出∠CFE=∠CEF.
(1)∵∠ACB=90°,CD是高,∠B=40°,
∴∠ACD+∠BAC=∠B+∠BAC=90°,
∴∠ACD=∠B=40°,∠BAC=50°,
又∵AE是角平分线,
∴∠BAE=∠CAF=25°,
∵∠CFE是△ACF的外角,∠CEF是△ABE的外角,
∴∠CFE=∠CAF+∠ACD=65°,∠CEF=∠B+∠BAE=65°,
故答案为:65;65;
(2)∠CFE和∠CEF相等,
理由:∵∠ACB=90°,CD是高,
∴∠ACD+∠BAC=∠B+∠BAC=90°,
∴∠ACD=∠B,
又∵AE是角平分线,
∴∠BAE=∠CAF,
∵∠CFE是△ACF的外角,∠CEF是△ABE的外角,
∴∠CFE=CAF+∠ACD,∠CEF=∠B+∠BAE,
∴∠CFE=∠CEF.


科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD⊥弦AB于M,AE⊥BD于E,交CD于N,连AC
(1)求证:AC=AN;
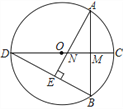
(2)若OM∶OC=3∶5,AB=5,求⊙O的半径;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全民读书月活动中,某校随机抽样调查了一部分学生本学期计划购买课外书的费用情况,根据图中的相关信息,解答下面问题;
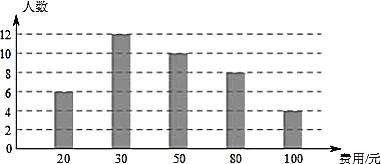
(1)这次调查获取的样本容量是________;
(2)由统计图可知,这次调查获取的样本数据的众数是________;中位数是________;
(3)若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你会玩“24点”游戏吗?从一副扑克牌(去掉大、小王)中任意抽取4张,根据牌面上的数字,添加+、一、×、÷和括号等符号进行运算,每张牌只能用一次,使得运算结果为24,其中A、J、Q、K分别代表1,11,12,13.
(1)小明抽到的是如下4张牌,你凑成24的算式是______(写出一个即可).

(2)现有四个有理数3、4、 -6、10,运用上述规则写出两种不同方法的运算式,使其结果等于24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A,B,把抛物线与线段AB围成的图形记为C1, 将Cl绕点B中心对称变换得C2, C2与x轴交于另一点C,将C2绕点C中心对称变换得C3, 连接C与C3的顶点,则图中阴影部分的面积为( )
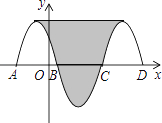
A. 32 B. 24 C. 36 D. 48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.

(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y<0时,x的取值范围;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=30°,点B在射线AM上,且 AB=6,点C在射线AN上.

(1)若△ABC是直角三角形,求AC的长;
(2)若△ABC是等腰三角形,则满足条件的C点有 个;
(3)设BC=x,当△ABC唯一确定时, 直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com