
科目:初中数学 来源: 题型:填空题
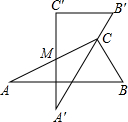 如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=5,则这块直角三角板顶点A、A′之间的距离等于2.5.
如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=5,则这块直角三角板顶点A、A′之间的距离等于2.5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
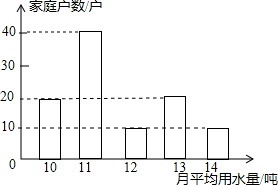 为了倡导“节约用水,从我做起”,某市政府决定对市直机关600户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭去年一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
为了倡导“节约用水,从我做起”,某市政府决定对市直机关600户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭去年一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,AC与BD相交于点O,E为AD上的一点,连接BE,点G在BE上,连结OG并延长交AD于点F,若∠FGE=45°.
如图,在正方形ABCD中,AC与BD相交于点O,E为AD上的一点,连接BE,点G在BE上,连结OG并延长交AD于点F,若∠FGE=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
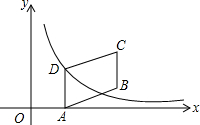 如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,则m=2.
如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,则m=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{m^2}+\sqrt{n^2}=\sqrt{{m^2}+{n^2}}$ | B. | $\sqrt{{a^2}-{b^2}}=\sqrt{a^2}-\sqrt{b^2}=a-b$ | ||
| C. | $\sqrt{3}×\sqrt{2}=\sqrt{3×2}$ | D. | $\sqrt{{{({-3})}^2}}=-3$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com