
【题目】如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径做圆,与BC相切于点C,点A作AD⊥BO交BO的延长线于点D,且∠AOD=∠BAD.

(1)求证:AB为⊙O的切线;
(2)若BC=6,tan∠ABC=![]() ,求⊙O的半径和AD的长.
,求⊙O的半径和AD的长.
【答案】(1)见解析;(2)3,![]() .
.
【解析】
(1)作OE⊥AB,先由∠AOD=∠BAD求得∠ABD=∠OAD,再由∠BCO=∠D=90°及∠BOC=∠AOD求得∠OBC=∠OAD=∠ABD,最后证△BOC≌△BOE得OE=OC,依据切线的判定可得;
(2)先求得∠EOA=∠ABC,在Rt△ABC中求得AC=8、AB=10,由切线长定理知BE=BC=6、AE=4、OE=3,继而得BO=3![]() ,再证△ABD∽△OBC,得
,再证△ABD∽△OBC,得![]() ,据此可得答案.
,据此可得答案.
(1)过点O作OE⊥AB于点E,

∵AD⊥BO于点D,
∴∠D=90°,
∴∠BAD+∠ABD=90°,
∠AOD+∠OAD=90°,
∵∠AOD=∠BAD,
∴∠ABD=∠OAD,
又∵BC为⊙O的切线,
∴AC⊥BC,
∴∠BOC=∠D=90°,
∵∠BOC=∠AOD,
∴∠OBC=∠OAD=∠ABD,
∴OE=OC,
∵OE⊥AB,
∴AB是⊙O的切线.
(2)∵∠ABC+∠BAC=90°
∠EOA+∠BAC=90°,
∴∠EOA=∠ABC,
∵tan∠ABC=![]() 、BC=6,
、BC=6,
∴AC=BCtan∠ABC=8,
则AB=10,
由(1)知BE=BC=6,
∴AE=4,
∵tan∠EOA=tan∠ABC=![]() ,
,
∴OE=3,![]() ,
,
∵∠ABD=∠OBC,∠D=∠ACB=90°,
∴△ABD∽△OBC,
∴![]() ,即
,即![]()
∴![]() .
.


科目:初中数学 来源: 题型:
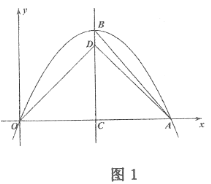
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,对称轴分别交抛物线和
,对称轴分别交抛物线和![]() 轴于点
轴于点![]() 和点
和点![]() ,以
,以![]() 为底边向上作等腰
为底边向上作等腰![]() .
.
(1)![]() ______;
______;![]() ______(用含
______(用含![]() 的代数式表示);
的代数式表示);
(2)如图1,当![]() 时,连接
时,连接![]() ,求
,求![]() 的值;
的值;
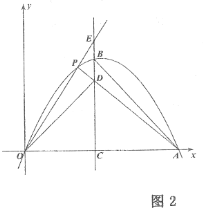
(3)点![]() 是抛物线
是抛物线![]() 段上任意一点,连接
段上任意一点,连接![]() 和
和![]() ,延长
,延长![]() 交对称轴于点
交对称轴于点![]() ,如图2,若
,如图2,若![]() ,
,![]() ,
,![]() 三点在一条直线上,当
三点在一条直线上,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
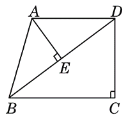
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD,连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)若 AD=25,BC=32,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
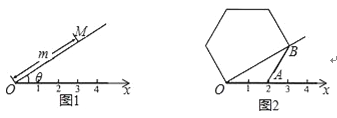
【题目】规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )
A.(![]() ,30°) B.(60°,
,30°) B.(60°,![]() )
)
C.(30°,4) D.(30°,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x.

(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;
(3)设△ADP与△PCB的外接圆的面积分别为S1、S2,若S=S1+S2,求S的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| … | -1 | 0 | 1 | 3 | … |
| … | -3 | 1 | 3 | 1 | … |
则下列判断中正确的是( )
A.抛物线开口向上B.抛物线与![]() 轴的交点在
轴的交点在![]() 轴负半轴上
轴负半轴上
C.当![]() 时,
时,![]() D.方程
D.方程![]() 的正根在3与4之间
的正根在3与4之间
查看答案和解析>>
科目:初中数学 来源: 题型:
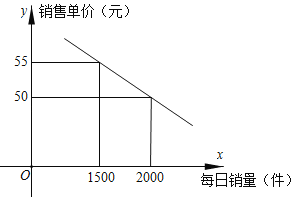
【题目】为倡导节能环保,降低能源消耗,提倡环保型新能源开发,造福社会.某公司研发生产一种新型智能环保节能灯,成本为每件40元.市场调查发现,该智能环保节能灯每件售价y(元)与每天的销售量为x(件)的关系如图,为推广新产品,公司要求每天的销售量不少于1000件,每件利润不低于5元.
(1)求每件销售单价y(元)与每天的销售量为x(件)的函数关系式并直接写出自变量x的取值范围;
(2)设该公司日销售利润为P元,求每天的最大销售利润是多少元?
(3)在试销售过程中,受国家政策扶持,毎销售一件该智能环保节能灯国家给予公司补贴m(m≤40)元.在获得国家每件m元补贴后,公司的日销售利润随日销售量的增大而增大,则m的取值范围是 (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
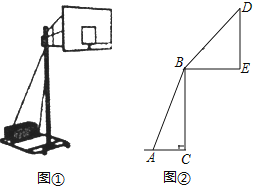
【题目】如图①,②分别是某款篮球架的实物图和示意图,已知支架AB的长为2.3m,支架AB与地面的夹角∠BAC=70°,BE的长为1.5m,篮板部支架BD与水平支架BE的夹角为46°,BC、DE垂直于地面,求篮板顶端D到地面的距离.(结果保留一位小数,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
查看答案和解析>>
科目:初中数学 来源: 题型:
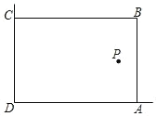
【题目】某兴趣小组想借助如图所示的直角墙角(两边足够长),用20m长的篱笆围成一个矩形ABCD(篱笆只围AB,BC两边),设ABxm.
(1)若花园的面积96m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是11m和5m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com