
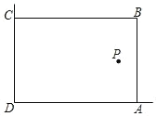
【题目】某兴趣小组想借助如图所示的直角墙角(两边足够长),用20m长的篱笆围成一个矩形ABCD(篱笆只围AB,BC两边),设ABxm.
(1)若花园的面积96m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是11m和5m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,O为AC上一点,以点O为圆心,OC为半径做圆,与BC相切于点C,点A作AD⊥BO交BO的延长线于点D,且∠AOD=∠BAD.

(1)求证:AB为⊙O的切线;
(2)若BC=6,tan∠ABC=![]() ,求⊙O的半径和AD的长.
,求⊙O的半径和AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店销售复习资料,已知每本复习资料进价为40元,市场调查发现:若以每本50元销售,平均每天可销售90本,在此基础上,若售价每提高1元,则平均每天少销售3本.设涨价后每本的售价为![]() 元,书店平均每天销售这种复习资料的利润为
元,书店平均每天销售这种复习资料的利润为![]() 元.
元.
(1)涨价后每本复习资料的利润为______元,平均每天可销售______本;
(2)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当复习资料每本售价为多少时,平均每天的利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
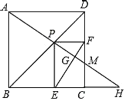
【题目】如图,点P是边长为2的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论:①MF=MC;②AH⊥EF;③AP2=PMPH; ④EF的最小值是![]() .其中正确的是________.(把你认为正确结论的序号都填上)
.其中正确的是________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
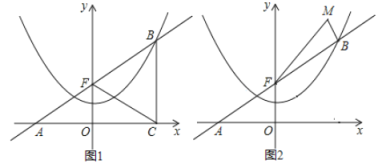
【题目】已知,抛物线y=ax2+c过点(-2,2)和点(4,5),点F(0,2)是y 轴上的定点,点B是抛物线上除顶点外的任意一点,直线l:y=kx+b经过点B、F且交x轴于点A.
(1)求抛物线的解析式;
(2)①如图1,过点B作BC⊥x轴于点C,连接FC,求证:FC平分∠BFO;
②当k= 时,点F是线段AB的中点;
(3)如图2, M(3,6)是抛物线内部一点,在抛物线上是否存在点B,使△MBF的周长最小?若存在,求出这个最小值及直线l的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组为了解我市气温变化情况,记录了今年月份连续![]() 天的最低气温(单位:℃):
天的最低气温(单位:℃):![]() .关于这组数据,下列结论不正确的是( )
.关于这组数据,下列结论不正确的是( )
A.平均数是![]() B.中位数是
B.中位数是![]() C.众数是
C.众数是![]() D.方差是
D.方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() .
.

(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N,
①点![]() 在线段
在线段![]() 上运动,若以
上运动,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上自由运动,若三个点
轴上自由运动,若三个点![]() ,
,![]() ,
,![]() 中恰有一点是其它两点所连线段的中点(三点重合除外),则称
中恰有一点是其它两点所连线段的中点(三点重合除外),则称![]() ,
,![]() ,
,![]() 三点为“共谐点”.请直接写出使得
三点为“共谐点”.请直接写出使得![]() ,
,![]() ,
,![]() 三点成为“共谐点”的
三点成为“共谐点”的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两名射击运动员的10次射击测试成绩的折线统计图.
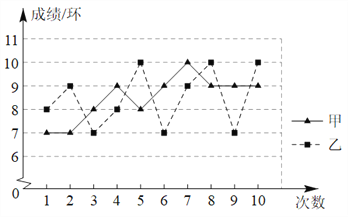
(1)根据折线图把下列表格补充完整;
运动员 | 平均数 | 中位数 | 众数 |
甲 | 8.5 | 9 | |
乙 | 8.5 |
(2)根据上述图表运用所学统计知识对甲、乙两名运动员的射击水平进行评价并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,点 D 为边 BC 的点,点 E、F 分别是边 AB、AC 上两点,且 EF∥BC,若 AE:EB=m,BD:DC=n,则( )
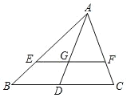
A.若 m>1,n>1,则 2S△AEF>S△ABDB.若 m>1,n<1,则 2S△AEF<S△ABD
C.若 m<1,n<1,则 2S△AEF<S△ABDD.若 m<1,n>1,则 2S△AEF<S△ABD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com