
【题目】如图,△ABC 中,点 D 为边 BC 的点,点 E、F 分别是边 AB、AC 上两点,且 EF∥BC,若 AE:EB=m,BD:DC=n,则( )
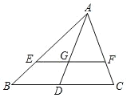
A.若 m>1,n>1,则 2S△AEF>S△ABDB.若 m>1,n<1,则 2S△AEF<S△ABD
C.若 m<1,n<1,则 2S△AEF<S△ABDD.若 m<1,n>1,则 2S△AEF<S△ABD
【答案】D
【解析】
根据相似三角形的判定与性质,得出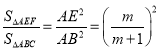 ,
,![]() ,从而建立等式关系,得出
,从而建立等式关系,得出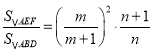 ,然后再逐一分析四个选项,即可得出正确答案 .
,然后再逐一分析四个选项,即可得出正确答案 .
解:∵EF∥BC,若AE:EB=m,BD:DC=n,
∴△AEF∽△ABC,
∴![]() ,
,
∴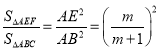 ,
,
∴![]() ,
,
∴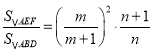
∴当m=1,n=1,即当E为AB中点,D为BC中点时,![]() ,
,
A.当m>1,n>1时,S△AEF与S△ABD同时增大,则![]() 或
或![]() ,即2
,即2![]()
或2![]() >
>![]() ,故A错误;
,故A错误;
B.当m>1,n <1,S△AEF增大而S△ABD减小,则![]() ,即2
,即2![]() ,故B错误;
,故B错误;
C.m<1,n<1,S△AEF与S△ABD同时减小,则![]() 或
或![]() ,即2
,即2![]() 或2
或2![]() <
<![]() ,故C错误;
,故C错误;
D.m<1,n>1,S△AEF减小而S△ABD增大,则![]() ,即2
,即2![]() <
<![]() ,故D正确 .
,故D正确 .
故选D .


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
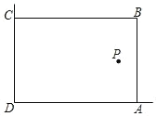
【题目】某兴趣小组想借助如图所示的直角墙角(两边足够长),用20m长的篱笆围成一个矩形ABCD(篱笆只围AB,BC两边),设ABxm.
(1)若花园的面积96m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是11m和5m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,![]() 中,
中,![]() ,动点
,动点![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,过点
运动,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的平行线,与过点
的平行线,与过点![]() 且与
且与![]() 垂直的直线交于点
垂直的直线交于点![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() (秒)
(秒)![]()

(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(2)求当点![]() 落在
落在![]() 边上时t的值;
边上时t的值;
(3)设![]() 与
与![]() 重合部分图形的面积为
重合部分图形的面积为![]() (平方单位),求
(平方单位),求![]() 与的
与的![]() 函数关系式;
函数关系式;
(4)连结![]() ,若将
,若将![]() 沿它自身的某边翻折,翻折前后的两个三角形形成菱形,直接写出此时
沿它自身的某边翻折,翻折前后的两个三角形形成菱形,直接写出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一元二次方程![]() 满足a+b+c=0,我们称这个方程为“凤凰”方程.已知
满足a+b+c=0,我们称这个方程为“凤凰”方程.已知![]() 是凤凰方程,且有两个相等的实数根,则下列正确的是( )
是凤凰方程,且有两个相等的实数根,则下列正确的是( )
A.a=cB.a=bC.b=cD.a=b=c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)

查看答案和解析>>
科目:初中数学 来源: 题型:
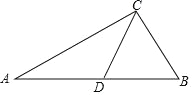
【题目】如图,在△ABC中,CD是边AB上的中线,∠B是锐角,sinB=![]() ,tanA=
,tanA=![]() ,AC=
,AC=![]() ,
,
(1)求∠B 的度数和 AB 的长.
(2)求 tan∠CDB 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 郑州外国语中学为了解学生课下阅读所用时间的情况,从各年级学生中随机抽查了一部分学生进行统计,下面是针对此次统计所制作的不完整的频数分布表和频数分布直方图,请根据图表信息回答下列问题:
组别 | 时间段(小时) | 频数 | 频率 |
1 | 0≤x<0.5 | 10 | 0.05 |
2 | 0.5≤x<1.0 | 20 | 0.10 |
3 | 1.0≤x<1.5 | 80 | b |
4 | 1.5≤x<2.0 | a | 0.35 |
5 | 2.0≤x<2.5 | 12 | 0.06 |
6 | 2.5≤x<3.0 | 8 | 0.04 |
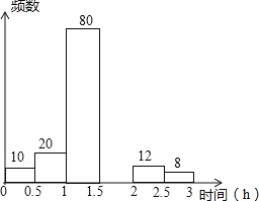
(1)表中a=______b=______;
(2)请补全频数分布直方图;
(3)样本中,学生日阅读所用时间的中位数落在第______组;
(4)该校共有学生3000人,请估计学生日阅读量不少于1.5小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点,过点
上一点,过点![]() 分别作
分别作![]() 与
与![]() 的垂线,过点
的垂线,过点![]() 作
作![]() 的垂线,得到矩形
的垂线,得到矩形![]() 和矩形
和矩形![]() ,则这两个矩形的面积之和的最大值是_________.
,则这两个矩形的面积之和的最大值是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com