
����Ŀ�� ��ͼ��![]() �У�
��![]() ������
������![]() ��
��![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶ����յ�
����λ���ȵ��ٶ����յ�![]() �˶�������
�˶�������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��ƽ���ߣ������
��ƽ���ߣ������![]() ����
����![]() ��ֱ��ֱ�߽��ڵ�
��ֱ��ֱ�߽��ڵ�![]() �����
�����![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() (��)
(��)![]()

��1���ú�![]() �Ĵ���ʽ��ʾ�߶�
�Ĵ���ʽ��ʾ�߶�![]() �ij���
�ij���
��2����![]() ����
����![]() ����ʱt��ֵ��
����ʱt��ֵ��
��3����![]() ��
��![]() �غϲ���ͼ�ε����Ϊ
�غϲ���ͼ�ε����Ϊ![]() (ƽ����λ)����
(ƽ����λ)����![]() ���
���![]() ������ϵʽ��
������ϵʽ��
��4������![]() ������
������![]() ����������ij�߷��ۣ�����ǰ��������������γ����Σ�ֱ��д����ʱ
����������ij�߷��ۣ�����ǰ��������������γ����Σ�ֱ��д����ʱ![]() ��ֵ.
��ֵ.
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��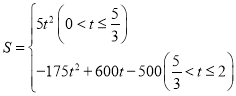 ����4��
����4��![]() ��
��![]() ��
��![]() .
.
��������
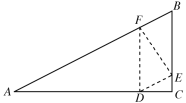
��1��������ɵ�DF��AC��EF��AB��DE��AB��Ȼ������ͬ�ǵ������ȿɵá�DFE=��A������֤����ADF�ס�FED���Ƴ�![]() ��Ȼ�������ADF�ס�ACB���ɷֱ��ú�t��ʽ�ӱ�ʾ��DF��AF��Ȼ��ɵ�DE��
��Ȼ�������ADF�ס�ACB���ɷֱ��ú�t��ʽ�ӱ�ʾ��DF��AF��Ȼ��ɵ�DE��
��2������![]() ����
����![]() ����ʱ������ADF�ס�DCE���г�����ʽ���DC=2t��Ȼ�����AC=20�з������t���ɣ�
����ʱ������ADF�ס�DCE���г�����ʽ���DC=2t��Ȼ�����AC=20�з������t���ɣ�
��3����![]() ʱ��
ʱ��![]() �����������������ʽ��⼴�ɣ���
�����������������ʽ��⼴�ɣ���![]() ʱ��
ʱ��![]() ����EH��AC��AC���ӳ����ڵ�H��EF��BC��N��DE��BC��M������ƽ���߷��߶γɱ����������NM���������������ʽ��⼴�ɣ�
����EH��AC��AC���ӳ����ڵ�H��EF��BC��N��DE��BC��M������ƽ���߷��߶γɱ����������NM���������������ʽ��⼴�ɣ�
��4����������������ij�߷��ۣ�����ǰ��������������γ����Σ���֪��ʱ![]() Ϊ���������Σ�Ȼ���������ۣ��ٵ�DE=CEʱ���ڵ�DC=CEʱ���۵�DE=DCʱ���ֱ��г�������t��ֵ����.
Ϊ���������Σ�Ȼ���������ۣ��ٵ�DE=CEʱ���ڵ�DC=CEʱ���۵�DE=DCʱ���ֱ��г�������t��ֵ����.
�⣺��1���������֪��DF��AC��EF��AB��DE��AB��
���ADF=90������EFA=90����
���DEF=90������DFA+��DFE =90����
�ߡ�DFA+��A =90����
���DFE=��A��
�ߡ�DEF=��ADF=90����
����ADF�ס�FED��
��![]() ��
��
�ߡ�C��90����
����ADF�ס�ACB��
��AC=20��BC=10��
��AB=![]() ��
��
��![]() ��
��![]() ��
��
�֡�AD=10t��
��DF=5t��AF=![]() ��
��
��![]() ��
��
��DE=![]() ��
��
��2������![]() ����
����![]() ����ʱ��
����ʱ��
��DE��AB��
����ADF�ס�DCE��
��![]() ��
��
�ɣ�1����֪��DE=![]() ��AF=
��AF=![]() ��AD=10t��
��AD=10t��
��DC=2t��
��10t+2t=20��
��ã�![]() ��
��
��3����DE=![]() ��
��
��EF=2DE=![]() ��
��
�൱![]() ʱ��
ʱ��![]() ��
��
��D����C��ʱ��t=20��10��2��
�൱![]() ʱ��
ʱ��![]() ��
��
��ͼ����EH��AC��AC���ӳ����ڵ�H��EF��BC��N��DE��BC��M��
ͬ��2���ɵ�DH=2t��
��CH=10t+2t-20=12t-20��DC=20-10t��
��BC��DF��
��![]() ��
��
��BC��EH��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]() ��
��
����������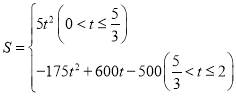 ��
��
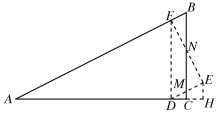
��4����������������ij�߷��ۣ�����ǰ��������������γ����Σ���֪��ʱ![]() Ϊ���������Σ�
����������
�ٵ�DE=CEʱ����ͼ����EH��DC�ڵ�H��
�ɣ�3���ɵ�DH=2t��
��DC=4t��
��10t+4t=20��
��ã�![]() ��
��
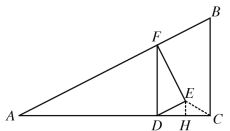
�ڵ�DC=CEʱ����ͼ����EH��AC��AC���ӳ����ڵ�H������CE��
�ɣ�3����֪��DE=![]() ��DH=2t��CH=12t-20��DC=20-10t��
��DH=2t��CH=12t-20��DC=20-10t��
��EH=t��
�ɹ��ɶ����ã�(12t-20)2+t2=(20-10t)2��
��ã�![]() ��
��
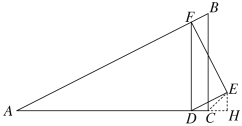
�۵�DE=DCʱ��
��DE=![]() ��DC=20-10t��
��DC=20-10t��
��![]() ��
��
��ã�![]() ��
��
������������![]() ��
��![]() ��
��![]() ʱ����
ʱ����![]() ����������ij�߷��ۣ�����ǰ��������������γ�����.
����������ij�߷��ۣ�����ǰ��������������γ�����.


 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������۸�ϰ���ϣ���֪ÿ����ϰ���Ͻ���Ϊ40Ԫ���г����鷢�֣�����ÿ��50Ԫ���ۣ�ƽ��ÿ�������90�����ڴ˻����ϣ����ۼ�ÿ���1Ԫ����ƽ��ÿ��������3�������Ǽۺ�ÿ�����ۼ�Ϊ![]() Ԫ�����ƽ��ÿ���������ָ�ϰ���ϵ�����Ϊ
Ԫ�����ƽ��ÿ���������ָ�ϰ���ϵ�����Ϊ![]() Ԫ��
Ԫ��
��1���Ǽۺ�ÿ����ϰ���ϵ�����Ϊ______Ԫ��ƽ��ÿ�������______����
��2����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3������ϰ����ÿ���ۼ�Ϊ����ʱ��ƽ��ÿ�����������������Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��������
��������![]() ������
������![]() ��
��![]() .
.

��1�����B������������ߵĽ���ʽ��
��2��M��m��0��Ϊx����һ�����㣬����M��ֱ��x���ֱ����ֱ��AB�������߷ֱ��ڵ�P��N��
����![]() ���߶�
���߶�![]() ���˶�������
���˶�������![]() ��
��![]() ��
��![]() �������������
Ϊ�������������![]() ���ƣ����
���ƣ����![]() �����ꣻ
�����ꣻ
����![]() ��
��![]() ���������˶�����������
���������˶�����������![]() ��
��![]() ��
��![]() ��ǡ��һ�����������������߶ε��е㣨�����غϳ��⣩�����
��ǡ��һ�����������������߶ε��е㣨�����غϳ��⣩�����![]() ��
��![]() ��
��![]() ����Ϊ����г����.��ֱ��д��ʹ��
����Ϊ����г����.��ֱ��д��ʹ��![]() ��
��![]() ��
��![]() �����Ϊ����г������
�����Ϊ����г������![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ǽס�����������˶�Ա��10��������Գɼ�������ͳ��ͼ.
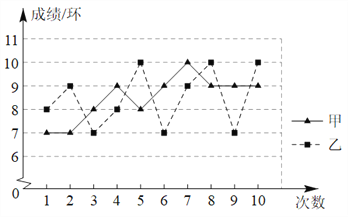
��1����������ͼ�����б���������
�˶�Ա | ƽ���� | ��λ�� | ���� |
�� | 8.5 | 9 | |
�� | 8.5 |
��2����������ͼ��������ѧͳ��֪ʶ�Լס��������˶�Ա�����ˮƽ�������۲�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ������
������![]() �ֱ���
�ֱ���![]() �ᡢ
�ᡢ![]() ��������ᣬ������
��������ᣬ������![]() ����
����![]() ���㣬��
���㣬��![]() Ϊ�����ߵĶ��㣬����
Ϊ�����ߵĶ��㣬����![]() .
.
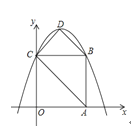
(1)��������ߵĽ���ʽ��
(2)ֱ��д���ı���![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
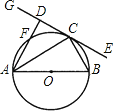
����Ŀ����ͼ����O��ֱ��AB��6��CΪԲ���ϵ�һ�㣬BC��3����C������O������GE����AD��GE�ڵ�D������O�ڵ�F��
��1����֤����ACG����B��
��2�������߶�AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���ͼ���A��B��C���㣬��A������Ϊ����1��0������B������Ϊ��4��0������C��y���������ϣ���AB��OC��

��1�����C�����ꣻ
��2������κ����Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC �У��� D Ϊ�� BC �ĵ㣬�� E��F �ֱ��DZ� AB��AC �����㣬�� EF��BC���� AE��EB��m��BD��DC��n���� ��
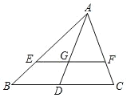
A.�� m��1��n��1���� 2S��AEF��S��ABDB.�� m��1��n��1���� 2S��AEF��S��ABD
C.�� m��1��n��1���� 2S��AEF��S��ABDD.�� m��1��n��1���� 2S��AEF��S��ABD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�Ա�У��2017��500��ѧ�����п��μ��������Բ���������е��飬��������1000��Ů��800�ײ��Գɼ����������Ƴɲ�������ͳ��ͼ����ͼ�٣�ͼ�ڣ��������ͳ��ͼ�ṩ����Ϣ���ش��������⣺
��1����У��ҵ���������� �ˣ�����ͳ��ͼ��a= ��

��2����ȫ����ͳ��ͼ��
��3����500��ѧ���������ȡһ��ѧ��������ѧ������ɼ���8�ּ�8�����µĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com