练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

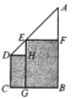
    【题目】如图，在四边形中，，，，，点是边上一点，过点分别作与的垂线，过点作的垂线，得到矩形和矩形，则这两个矩形的面积之和的最大值是_________．

    【答案】

    【解析】

    延长DH交AB于点I，则DI⊥AB，利用矩形和等腰直角三角形的性质，求出CD的长度，然后求出S与x的关系式，利用二次函数的性质，即可得到答案.

    解：根据题意，，

    延长DH交AB于点I，则DI⊥AB，

    ∴四边形BCDI是矩形，

    ∴DI=BC=3，CD=BI，

    由，DI⊥AB，

    ∴△ADI是等腰直角三角形，

    ∴AI=DI=3，

    ∴CD=BI=，

    ∵△AEF是等腰直角三角形，

    ∴EF=AF；

    设EF=AF=x，则FI=3-x，

    ∴这两个矩形的面积之和为：，

    即；

    ∵，

    ∴当时，这两个矩形的面积之和有最大值，最大值为；

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC 中，点 D 为边 BC 的点，点 E、F 分别是边 AB、AC 上两点，且 EF∥BC，若 AE：EB＝m，BD：DC＝n，则（ ）

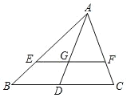
    A.若 m＞1，n＞1，则 2S△AEF＞S△ABDB.若 m＞1，n＜1，则 2S△AEF＜S△ABD

    C.若 m＜1，n＜1，则 2S△AEF＜S△ABDD.若 m＜1，n＞1，则 2S△AEF＜S△ABD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学对本校初2017届500名学生中中考参加体育加试测试情况进行调查，根据男生1000米及女生800米测试成绩整理，绘制成不完整的统计图，（图①，图②），请根据统计图提供的信息，回答下列问题：

    （1）该校毕业生中男生有 人；扇形统计图中a= ；

    （2）补全条形统计图；

    （3）若500名学生中随机抽取一名学生，这名学生该项成绩在8分及8分以下的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】自2017年3月起，成都市中心城区居民用水实行以户为单位的三级阶梯收费办法：

    第I级：居民每户每月用水18吨以内含18吨每吨收水费a元；

    第Ⅱ级：居民每户每月用水超过18吨但不超过25吨，未超过18吨的部分按照第Ⅰ级标准收费，超过部分每吨收水费b元；

    第Ⅲ级：居民每户每月用水超过25吨，未超过25吨的部分按照第I、Ⅱ级标准收费，超过部分每吨收水费c元．

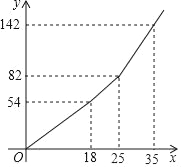
    设一户居民月用水x吨，应缴水费为y元，y与x之间的函数关系如图所示

    （1）根据图象直接作答：a＝　 　，b＝　 　；

    （2）求当x≥25时y与x之间的函数关系；

    （3）把上述水费阶梯收费办法称为方案①，假设还存在方案②：居民每户月用水一律按照每吨4元的标准缴费，请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案．（写出过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

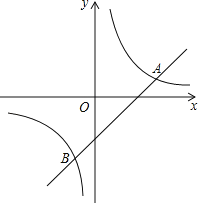
    【题目】如图，在平面直角坐标系xOy中，直线y=x﹣2与双曲线y=(k≠0)相交于A，B两点，且点A的横坐标是3．

    (1)求k的值；

    (2)过点P(0，n)作直线，使直线与x轴平行，直线与直线y=x﹣2交于点M，与双曲线y= (k≠0)交于点N，若点M在N右边，求n的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是的外接圆，且，延长至点，使得，点是上的一个动点，连结，，．

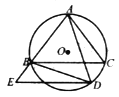
    （1）当时，求证：；

    （2）若，则：

    ①求的半径；

    ②当为直角三角形时，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（思考题）

    阅读下面的情景对话，然后解答问题：

    老师：我们新定义一种三角形，两边平方和等于第三边平方的2倍的三角形叫做奇异三角形．

    小华：等边三角形一定是奇异三角形；

    小明：那直角三角形是否存在奇异三角形呢？

    （1）①根据“奇异三角形”的定义，小红得出命题：“等边三角形一定是奇异三角形”，请判断小红提出的命题是否正确，并填空：命题 （填“正确”或“不正确”），不要说嘛理由．

    ②若某三角形的三边长分别是2、4、，则△ABC是奇异三角形吗？ （填“是”或“不是”），不要说嘛理由．

    （2）在Rt△ABC中，两边长分别是a=5、c=10，这个三角形是否是奇异三角形？请说明理由．

    （3）在Rt△ABC中，∠C=90°，AB=c，AC=b，BC=a，且b＞a，若Rt△ABC是奇异三角形，求a：b：c的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题探究：

    （1）如图①所示是一个半径为，高为4的圆柱体和它的侧面展开图，AB是圆柱的一条母线，一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点，求蚂蚁爬行的最短路程．（探究思路：将圆柱的侧面沿母线AB剪开，它的侧面展开图如图①中的矩形则蚂蚁爬行的最短路程即为线段的长）

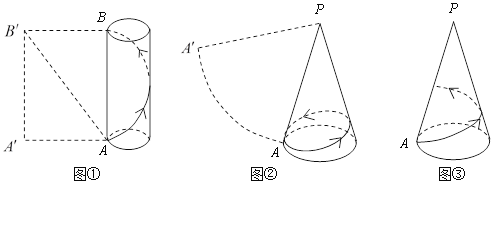
    （2）如图②所示是一个底面半径为，母线长为4的圆锥和它的侧面展开图，PA是它的一条母线，一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点，求蚂蚁爬行的最短路程．

    （3）如图③所示，在②的条件下，一只蚂蚁从A点出发沿圆锥的侧面爬行一周到达母线PA上的一点，求蚂蚁爬行的最短路程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知在Rt△OAC中，∠OCA=90°，O为坐标原点，直角顶点C在x轴的正半轴上，反比例函数y=（k＞0）在第一象限的图象经过OA的中点B，交AC于点D，连接OD．若∠A=∠COD，则直线OA的解析式为______．

    查看答案和解析>>

    同步练习册答案