
ЁОЬтФПЁПЮЊГЋЕМНкФмЛЗБЃЃЌНЕЕЭФмдДЯћКФЃЌЬсГЋЛЗБЃаЭаТФмдДПЊЗЂЃЌдьИЃЩчЛсЃЎФГЙЋЫОбаЗЂЩњВњвЛжжаТаЭжЧФмЛЗБЃНкФмЕЦЃЌГЩБОЮЊУПМў40дЊЃЎЪаГЁЕїВщЗЂЯжЃЌИУжЧФмЛЗБЃНкФмЕЦУПМўЪлМлyЃЈдЊЃЉгыУПЬьЕФЯњЪлСПЮЊxЃЈМўЃЉЕФЙиЯЕШчЭМЃЌЮЊЭЦЙуаТВњЦЗЃЌЙЋЫОвЊЧѓУПЬьЕФЯњЪлСПВЛЩйгк1000МўЃЌУПМўРћШѓВЛЕЭгк5дЊЃЎ
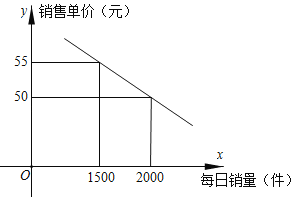
ЃЈ1ЃЉЧѓУПМўЯњЪлЕЅМлyЃЈдЊЃЉгыУПЬьЕФЯњЪлСПЮЊxЃЈМўЃЉЕФКЏЪ§ЙиЯЕЪНВЂжБНгаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЩшИУЙЋЫОШеЯњЪлРћШѓЮЊPдЊЃЌЧѓУПЬьЕФзюДѓЯњЪлРћШѓЪЧЖрЩйдЊЃП
ЃЈ3ЃЉдкЪдЯњЪлЙ§ГЬжаЃЌЪмЙњМвеўВпЗіГжЃЌАЯњЪлвЛМўИУжЧФмЛЗБЃНкФмЕЦЙњМвИјгшЙЋЫОВЙЬљmЃЈmЁм40ЃЉдЊЃЎдкЛёЕУЙњМвУПМўmдЊВЙЬљКѓЃЌЙЋЫОЕФШеЯњЪлРћШѓЫцШеЯњЪлСПЕФдіДѓЖјдіДѓЃЌдђmЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЈжБНгаДГіНсЙћЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉКЏЪ§ЙиЯЕЪНЮЊyЃНЉ![]() x+70ЃЌздБфСПxЕФШЁжЕЗЖЮЇ1000ЁмxЁм2500ЃЛЃЈ2ЃЉУПЬьЕФзюДѓЯњЪлРћШѓЪЧ22500дЊЃЛЃЈ3ЃЉmЕФШЁжЕЗЖЮЇЪЧЃК20ЁмmЁм40ЃЎ
x+70ЃЌздБфСПxЕФШЁжЕЗЖЮЇ1000ЁмxЁм2500ЃЛЃЈ2ЃЉУПЬьЕФзюДѓЯњЪлРћШѓЪЧ22500дЊЃЛЃЈ3ЃЉmЕФШЁжЕЗЖЮЇЪЧЃК20ЁмmЁм40ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЙЙНЈЖўДЮКЏЪ§ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЙЙНЈЖўДЮКЏЪ§ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪМДПЩНтОіЮЪЬтЃЛ
НтЃКЃЈ1ЃЉЩшУПМўЯњЪлЕЅМлyЃЈдЊЃЉгыУПЬьЕФЯњЪлСПЮЊxЃЈМўЃЉЕФКЏЪ§ЙиЯЕЪНЮЊyЃНkx+bЃЌ
АбЃЈ1500ЃЌ55ЃЉгыЃЈ2000ЃЌ50ЃЉДњШыyЃНkx+bЕУЃЌ
![]() ЃЌ
ЃЌ
НтЕУЃК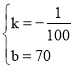 ЃЌ
ЃЌ
ЁрУПМўЯњЪлЕЅМлyЃЈдЊЃЉгыУПЬьЕФЯњЪлСПЮЊxЃЈМўЃЉЕФКЏЪ§ЙиЯЕЪНЮЊyЃНЉ![]() x+70ЃЌ
x+70ЃЌ
ЕБyЁн45ЪБЃЌЉ![]() x+70Ён45ЃЌНтЕУЃКxЁм2500ЃЌ
x+70Ён45ЃЌНтЕУЃКxЁм2500ЃЌ
ЁрздБфСПxЕФШЁжЕЗЖЮЇ1000ЁмxЁм2500ЃЛ
ЃЈ2ЃЉИљОнЬтвтЕУЃЌPЃНЃЈyЉ40ЃЉxЃНЃЈЉ![]() x+70Љ40ЃЉxЃНЉ
x+70Љ40ЃЉxЃНЉ![]() x2+30xЃНЉ
x2+30xЃНЉ![]() ЃЈxЉ1500ЃЉ2+22500ЃЌ
ЃЈxЉ1500ЃЉ2+22500ЃЌ
ЁпЉ![]() ЃМ0ЃЌPгазюДѓжЕЃЌ
ЃМ0ЃЌPгазюДѓжЕЃЌ
ЕБxЃМ1500ЪБЃЌPЫцxЕФдіДѓЖјдіДѓЃЌ
ЁрЕБxЃН1500ЪБЃЌPЕФзюДѓжЕЮЊ22500дЊЃЌ
Д№ЃКУПЬьЕФзюДѓЯњЪлРћШѓЪЧ22500дЊЃЛ
ЃЈ3ЃЉгЩЬтвтЕУЃЌPЃНЃЈЉ![]() x+70Љ40+mЃЉxЃНЉ
x+70Љ40+mЃЉxЃНЉ![]() x2+ЃЈ30+mЃЉxЃЌ
x2+ЃЈ30+mЃЉxЃЌ
ЁпЖдГЦжсЮЊxЃН50ЃЈ30+mЃЉЃЌ
Ёп1000ЁмxЁм2500ЃЌ
ЁрxЕФШЁжЕЗЖЮЇдкЖдГЦжсЕФзѓВрЪБPЫцxЕФдіДѓЖјдіДѓЃЌ
50ЃЈ30+mЃЉЁн2500ЃЌ
НтЕУЃКmЁн20ЃЌ
ЁрmЕФШЁжЕЗЖЮЇЪЧЃК20ЁмmЁм40ЃЎ
ЙЪД№АИЮЊЃК20ЁмmЁм40ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбвЛИіСПНЧЦїгывЛПщ30ЁуЃЈЁЯCABЃН30ЁуЃЉНЧЕФШ§НЧАхЦДдквЛЦ№ЃЌШ§НЧАхЕФаББпABгыСПНЧЦїЫљдкдВЕФжБОЖMNжиКЯЃЌЯжгаЩфЯпCPШЦЕуCДгCAПЊЪМбиЫГЪБеыЗНЯђвдУПУы2ЁуЕФЫйЖШа§зЊЕНгыCBжиКЯЃЌОЭЭЃжЙа§зЊЃЎдка§зЊЙ§ГЬжаЃЌЩфЯпCPгыСПНЧЦїЕФАыдВЛЁНЛгкEЃЎСЌНгBEЃЎ
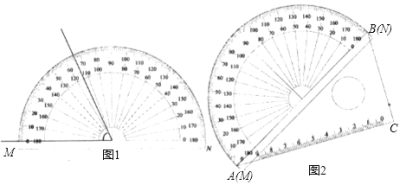
ЃЈ1ЃЉЩша§зЊxУыКѓЃЌЕуEДІЕФЖСЪ§ЮЊyЁуЃЌдђyгыxЕФКЏЪ§ЙиЯЕЪН________ЃЎ
ЃЈ2ЃЉЕБCPа§зЊ________УыЪБЃЌЁїBCEЪЧЕШбќШ§НЧаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬx2Љ6xЉk2=0ЃЈkЮЊГЃЪ§ЃЉЃЎ
ЃЈ1ЃЉЧѓжЄЃКЗНГЬгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ
ЃЈ2ЃЉЩшx1ЃЌx2ЮЊЗНГЬЕФСНИіЪЕЪ§ИљЃЌЧвx1+2x2=14ЃЌЪдЧѓГіЗНГЬЕФСНИіЪЕЪ§ИљКЭkЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
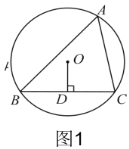
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌOЮЊACЩЯвЛЕуЃЌвдЕуOЮЊдВаФЃЌOCЮЊАыОЖзідВЃЌгыBCЯрЧагкЕуCЃЌЕуAзїADЁЭBOНЛBOЕФбгГЄЯпгкЕуDЃЌЧвЁЯAOD=ЁЯBADЃЎ

ЃЈ1ЃЉЧѓжЄЃКABЮЊЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєBC=6ЃЌtanЁЯABC=![]() ЃЌЧѓЁбOЕФАыОЖКЭADЕФГЄЃЎ
ЃЌЧѓЁбOЕФАыОЖКЭADЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌ![]() ЪЧ
ЪЧ![]() ЕФФкНгШ§НЧаЮЃЌ
ЕФФкНгШ§НЧаЮЃЌ![]() гкЕу
гкЕу![]() ЃЎЧыНігУЮоПЬЖШЕФжБГпЃЌЛГі
ЃЎЧыНігУЮоПЬЖШЕФжБГпЃЌЛГі![]() жа
жа![]() ЕФЦНЗжЯпЃЎЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉЃЎ
ЕФЦНЗжЯпЃЎЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉЃЎ
 ЁЁЁЁЁЁ
ЁЁЁЁЁЁ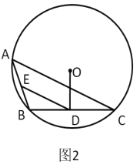
ЃЈ2ЃЉШчЭМ2ЃЌ![]() ЮЊ
ЮЊ![]() ЕФЭтНгдВЃЌ
ЕФЭтНгдВЃЌ![]() ЪЧЗЧжБОЖЕФЯвЃЌ
ЪЧЗЧжБОЖЕФЯвЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЪЧЯв
ЪЧЯв![]() ЩЯвЛЕуЃЌЧв
ЩЯвЛЕуЃЌЧв![]() ЃЌЧыНігУЮоПЬЖШЕФжБГпЃЌШЗЖЈГі
ЃЌЧыНігУЮоПЬЖШЕФжБГпЃЌШЗЖЈГі![]() ЕФФкаФ
ЕФФкаФ![]() ЃЎЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉ
ЃЎЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзПкДќжазАга2ИіЯрЭЌЕФаЁЧђЃЌЫќУЧЗжБ№аДгаЪ§зж1КЭ2ЃЛввПкДќжазАга3ИіЯрЭЌЕФаЁЧђЃЌЫќУЧЗжБ№аДгаЪ§зж3ЃЌ4КЭ5ЃЎРћгУЛЪїзДЭМЛђСаБэЧѓЯТСаЪТМўЕФИХТЪЃЎ
ЃЈ1ЃЉДгСНИіПкДќжаИїЫцЛњШЁГі1ИіаЁЧђЃЌЧЁКУСНИіЖМЪЧЦцЪ§ЃЛ
ЃЈ2ЃЉШєБћПкДќжазАга2ИіЯрЭЌЕФаЁЧђЃЌЫќУЧЗжБ№аДгаЪ§зж6КЭ7ЃЌДгШ§ИіПкДќжаИїЫцЛњШЁГівЛИіаЁЧђЃЌЧЁКУШ§ИіЖМЪЧЦцЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
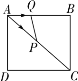
ЁОЬтФПЁПШчЭМЃЌвбжЊдкОиаЮ ABCD жаЃЌABЃН4ЃЌADЃН3ЃЌСЌНг ACЃЌЖЏЕу Q вдУПУы 1 ИіЕЅЮЛЕФЫйЖШби AЁњBЁњC ЯђЕу C дШЫйдЫЖЏЃЌЭЌЪБЕу P вдУПУы 2 ИіЕЅЮЛЕФЫйЖШби AЁњCЁњD ЯђЕу D дШЫйдЫЖЏЃЌСЌНг PQЃЌЕБЕу P ЕНДяжеЕу D ЪБЃЌЭЃжЙдЫ ЖЏЃЌЩшЁїAPQ ЕФУцЛ§ЮЊ SЃЌдЫЖЏЪБМфЮЊ t УыЃЌдђ S гы t КЏЪ§ЙиЯЕЕФЭМЯѓДѓжТЮЊЃЈ ЃЉ
A.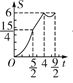 B.
B.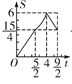 C.
C. D.
D.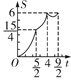
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪщЕъЯњЪлИДЯАзЪСЯЃЌвбжЊУПБОИДЯАзЪСЯНјМлЮЊ40дЊЃЌЪаГЁЕїВщЗЂЯжЃКШєвдУПБО50дЊЯњЪлЃЌЦНОљУПЬьПЩЯњЪл90БОЃЌдкДЫЛљДЁЩЯЃЌШєЪлМлУПЬсИп1дЊЃЌдђЦНОљУПЬьЩйЯњЪл3БОЃЎЩшеЧМлКѓУПБОЕФЪлМлЮЊ![]() дЊЃЌЪщЕъЦНОљУПЬьЯњЪлетжжИДЯАзЪСЯЕФРћШѓЮЊ
дЊЃЌЪщЕъЦНОљУПЬьЯњЪлетжжИДЯАзЪСЯЕФРћШѓЮЊ![]() дЊЃЎ
дЊЃЎ
ЃЈ1ЃЉеЧМлКѓУПБОИДЯАзЪСЯЕФРћШѓЮЊ______дЊЃЌЦНОљУПЬьПЩЯњЪл______БОЃЛ
ЃЈ2ЃЉЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕБИДЯАзЪСЯУПБОЪлМлЮЊЖрЩйЪБЃЌЦНОљУПЬьЕФРћШѓзюДѓЃПзюДѓРћШѓЮЊЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌХзЮяЯп
ЃЌХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌ
ЃЌ![]() .
.

ЃЈ1ЃЉЧѓЕуBЕФзјБъКЭХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉMЃЈmЃЌ0ЃЉЮЊxжсЩЯвЛИіЖЏЕуЃЌЙ§ЕуMДЙжБгкxжсЕФжБЯпгыжБЯпABКЭХзЮяЯпЗжБ№НЛгкЕуPЁЂNЃЌ
ЂйЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯдЫЖЏЃЌШєвд
ЩЯдЫЖЏЃЌШєвд![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЖЅЕуЕФШ§НЧаЮгы
ЮЊЖЅЕуЕФШ§НЧаЮгы![]() ЯрЫЦЃЌЧѓЕу
ЯрЫЦЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЂкЕу![]() дк
дк![]() жсЩЯздгЩдЫЖЏЃЌШєШ§ИіЕу
жсЩЯздгЩдЫЖЏЃЌШєШ§ИіЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жаЧЁгавЛЕуЪЧЦфЫќСНЕуЫљСЌЯпЖЮЕФжаЕуЃЈШ§ЕужиКЯГ§ЭтЃЉЃЌдђГЦ
жаЧЁгавЛЕуЪЧЦфЫќСНЕуЫљСЌЯпЖЮЕФжаЕуЃЈШ§ЕужиКЯГ§ЭтЃЉЃЌдђГЦ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§ЕуЮЊЁАЙВаГЕуЁБ.ЧыжБНгаДГіЪЙЕУ
Ш§ЕуЮЊЁАЙВаГЕуЁБ.ЧыжБНгаДГіЪЙЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§ЕуГЩЮЊЁАЙВаГЕуЁБЕФ
Ш§ЕуГЩЮЊЁАЙВаГЕуЁБЕФ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com