练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
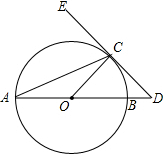
    15．如图，AB⊙O的直径，ED切⊙O于点C，交AB的延长线于点D，且CO=CD，则∠ECA=（　　）
    A．30°B．45°C．60°D．67.5°

    分析 根据等腰三角形性质和三角形外角性质求出∠COD=2∠A，求出∠D=∠COD，根据切线性质求出∠OCD=90°，即可求出答案；

    解答 解：∵OA=OC
    ∴∠A=∠ACO，
    ∴∠COD=∠A+∠ACO=2∠A，
    ∵OC=CD，
    ∴∠D=∠COD，
    ∵ED切⊙O于C，
    ∴∠OCD=90°，
    ∴∠D=∠COD=45°，
    ∠A=$\frac{1}{2}$∠COD=22，.5°，
    ∴∠ECA=∠A+∠D=67.5°．
    故选D．

    点评 本题考查了切线的性质，等腰三角形性质，三角形的外角性质的应用，熟记定理是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

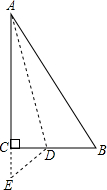    5．如右图，有一块直角三角形纸片，∠C=90°，AC=12cm，BC=5cm，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CE的长为1cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．在tan45°，sin60°，3.14，π，0.101001，$\frac{22}{7}$中，无理数的个数是（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．请用科学的方法证明圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．以下说法正确的有（　　）
    ①顺次连接等腰梯形四边中点所得的四边形一定是菱形；②$\sqrt{27}$与$\sqrt{\frac{1}{3}}$是同类二次根式；③长度等于半径的弦所对的圆周角为30°；④反比例函数y=-$\frac{2}{x}$，当x＜0时，y随x的增大而增大．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．图“E”中同旁内角有3对．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．（1）计算：（$\sqrt{5}$+$\sqrt{3}$）-（2$\sqrt{3}$+$\sqrt{5}$）
    （2）计算：（$\sqrt{3}$）2+4×$\sqrt{（-\frac{1}{2}）^{2}}$-（-2）3+$\root{3}{27}$
    （3）化简：|a-π|+|a-$\sqrt{2}$|-|2-π|（$\sqrt{2}$＜a＜π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

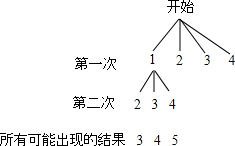    4．在不透明的袋子中有四张标着数字1，2，3，4 的卡片，这些卡片除数字外都相同．甲同学按照一定的规则抽出两张卡片，并把卡片上的数字相加．如图是他所画的树状图的一部分．
    （1）由如图分析，甲同学的游戏规则是：从袋子中随机抽出一张卡片后不放回（填“放回”或“不放回”），再随机抽出一张卡片；
    （2）帮甲同学完成树状图；
    （3）求甲同学两次抽到的数字之和为偶数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．先化简，再求值：（a-$\frac{2ab-{b}^{2}}{a}$）÷$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+ab}$，其中a=$\sqrt{3}$+1，b=$\sqrt{3}$-1．

    查看答案和解析>>

    同步练习册答案