
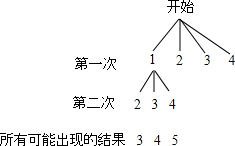
 在不透明的袋子中有四张标着数字1,2,3,4 的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.如图是他所画的树状图的一部分.
在不透明的袋子中有四张标着数字1,2,3,4 的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.如图是他所画的树状图的一部分.分析 (1)根据小明画出的树形图知数字1在第一次中出现,但没有在第二次中出现可以判断;
(2)根据本实验是一个不放回试验作出树状图即可;
(3)根据树状图利用概率公式求解即可.
解答 解:(1)观察树状图知:第一次摸出的数字没有在第二次中出现,
∴甲同学的实验是一个不放回实验,
故答案为:不放回;
(2)补全树状图为:
(3)由树状图得:
共有12种情况,两次抽到的数字之和为偶数的有4种,
故P(两次抽到的数字之和为偶数)=$\frac{4}{12}$=$\frac{1}{3}$.
点评 本题考查了列表法和树状图法,利用列表法或树状图法展示某一随机事件中所有等可能出现的结果数n,再找出其中某一事件所出现的可能数m,然后根据概率的定义可计算出这个事件的概率$\frac{m}{n}$.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
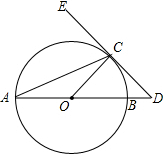 如图,AB⊙O的直径,ED切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠ECA=( )
如图,AB⊙O的直径,ED切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠ECA=( )| A. | 30° | B. | 45° | C. | 60° | D. | 67.5° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com