
【题目】一块含45°的直角三角板ABC, AB=AC, ∠BAC=90°, 点D为射线CB上一点,且不与点C,点B重合,连接AD.过点A作线段AD的垂线l,在直线l上,截取AE=AD(点E与点C在直线AD的同侧),连接CE.
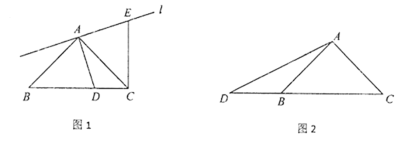
(1)当点D在线段CB上时,如图1,线段CE与BD的数量关系为____________,位置关系为___________;
(2)当点D在线段CB的延长线上时,如图2,
①请将图形补充完整;
②(1)中的结论是否仍成立?如果成立,请证明;如果不成立,请说明理由.
【答案】(1)CE=BD, CE⊥BD;(2)①见解析,②成立,理由见解析
【解析】
(1)在图1中证明△ABD≌△ACE,得到CE=BD,∠B=∠ACE=45°即可得到∠BCE=90°,即CE⊥BD;
(2)①根据题意,画出图形即可;
②与(1)同理,证明△ADB≌△AEC,然后得到CE=BD,然后得到∠ABC=∠ACB=45°,然后得到∠BCE=90°,即CE⊥BD.
证明:(1)∵AD⊥l,
∴∠DAE=∠BAC=90°,
∴∠BAD+∠DAC=∠DAC+∠CAE=90°,
∴∠BAD=∠CAE,
∵AD=AE,AB=AC,
∴△ABD≌△ACE,
∴CE=BD,∠B=∠ACE=45°,
∴∠ACB+∠ACE=45°+45°=90°,
∴∠BCE=90°,即CE⊥BD;
故答案为:CE=BD,CE⊥BD;
(2)①补全图形,如图:
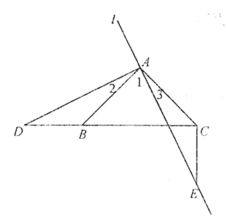
②CE=BD,CE⊥BD仍成立;
证明:∵AD⊥AE
∴∠DAE=90°
∵∠BAC=90°
∴∠DAE![]() ∠1=∠BAC
∠1=∠BAC![]() ∠1
∠1
即∠2=∠3
∵AB=AC, AD=AE
∴△ADB≌△AEC
∴CE=BD,∠ACE=∠ABD
∵∠ABC=∠ACB=45°
∴∠ACE=∠ABD=135°
∴∠DCE=∠ACE![]() ∠ACB=90°
∠ACB=90°
∴CE⊥BD.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.

(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在长度为1个单位的小正方形组成的网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)△ABC的面积为________;
(3)在直线l上找一点P,使PB+PC的长最短,则这个最短长度为________个单位长度.(在图形中标出点P)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,对任意一个正整数n都可以进行这样的分解:n=p![]() q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p
q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p![]() q是n的最佳分解,并规定:F(n)=
q是n的最佳分解,并规定:F(n)=![]() ,例如12可以分解为1
,例如12可以分解为1![]() 12,2
12,2![]() 6或3
6或3![]() 4,因为12-1>6-2>4-3,所以3
4,因为12-1>6-2>4-3,所以3![]() 4是最佳分解,所以F(n)=
4是最佳分解,所以F(n)=![]() 。
。
(1)如果一个正整数![]() 是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
(2)如果一个两位正整数t,t=10x+y (1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们就称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方正确的是( )
A. 方程x2-6x-5=0,可化为(x-3)2=4
B. 方程y2-2y-2 015=0,可化为(y-1)2=2 015
C. 方程a2+8a+9=0,可化为(a+4)2=25
D. 方程2x2-6x-7=0,可化为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=12cm,∠B=∠C,BC=8cm,点D为AB的中点.
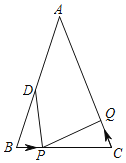
(1)如果点P在线段BC上以2cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过 后,点P与点Q第一次在△ABC的 边上相遇?(在横线上直接写出答案,不必书写解题过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com