
| A. | △ABC中,若∠A=∠C-∠B,则△ABC是直角三角形 | |
| B. | △ABC中,若a2=b2-c2,则△ABC是直角三角形 | |
| C. | △ABC中,若a:b:c=5:12:13,则△ABC是直角三角形 | |
| D. | △ABC中,若∠A,∠B,∠C的度数比是3:4:5,则△ABC是直角三角形 |
分析 根据直角三角形的定义和勾股定理的逆定理运用方程的思想对各个选项进行分析证明,得到答案.
解答 解:△ABC中,若∠A=∠C-∠B,则∠A+∠B=∠C,∠C=90°,△ABC是直角三角形,A正确;
△ABC中,若a2+c2=b2,由勾股定理的逆定理可知,△ABC是直角三角形,B正确;
△ABC中,若a:b:c=5:12:13,
设a、b、c分别为5x、12x、13x,
∵(5x)2+(12x)2=(13x)2,
则△ABC是直角三角形,C正确;
△ABC中,若∠A,∠B,∠C的度数比是3:4:5,
设∠A,∠B,∠C的度数分别为3x:4x:5x,
则3x+4x+5x=180°,
解得,x=15°,则3x=45°,4x=60°,5x=75°,
则△ABC不是直角三角形,
故选:D.
点评 本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题,根据真假三角形的判定方法,判断符合各个选项条件的三角形是否是真假三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
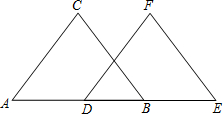 看图填空:已知:如图,BC∥EF,AD=BE,BC=EF,试说明△ABC≌△DEF
看图填空:已知:如图,BC∥EF,AD=BE,BC=EF,试说明△ABC≌△DEF查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:填空题
已知关于x的方程kx2+(k+2) x+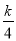 =0有两个不相等的实数根,则k的取值范围是__________.
=0有两个不相等的实数根,则k的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
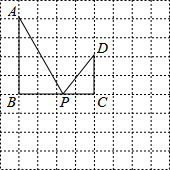 在如图所示的方格中,点A,B,C,D都在格点上,且AB=BC=2CD=4,P是线段BC上的动点,连结AP,DP.
在如图所示的方格中,点A,B,C,D都在格点上,且AB=BC=2CD=4,P是线段BC上的动点,连结AP,DP.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①④ | C. | ①②③ | D. | ①②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com