
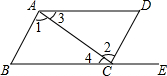
 如图,给出下列条件:其中,能推出AB∥DC的是( )
如图,给出下列条件:其中,能推出AB∥DC的是( )| A. | ①④ | B. | ②③ | C. | ①③ | D. | ①③④ |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运输工具 | 途中费用(元/km) | 装卸总费用(元) |
| 火车 | 4 | 2000 |
| 汽车 | 8 | 1000 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,0) | B. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$ | D. | 以上答案都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在第1个△ABA1中,∠B=20°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2A3D;…,按此做法进行下去,第三个三角形中,以A3为顶点的底角的度数为20°;第n个三角形中以An为顶点的底角的度数为$\frac{80°}{{2}^{n-1}}$.
如图,在第1个△ABA1中,∠B=20°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2A3D;…,按此做法进行下去,第三个三角形中,以A3为顶点的底角的度数为20°;第n个三角形中以An为顶点的底角的度数为$\frac{80°}{{2}^{n-1}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com