
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=10,并求出此时P点的坐标;
(3)设(1)中的抛物线交y轴交于C点,在该抛物线的对称轴上是否存在点Q,使△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
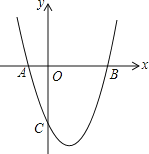
【答案】(1)y=x2-2x-3;(2)P点的坐标为(-2,5)或(4,5);(3)点Q的坐标为(1,-2).
【解析】
(1)根据抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点得到关于b和c的二元一次方程组,解方程组求出b和c的值即可;
(2)设动点P的坐标为(m,m2-2m-3),根据面积公式求出m的值即可;
(3)设点C关于对称轴的对称点为C′,连接AC′,直线AC′与对称轴的交点即为满足题意的Q点.
(1)∵抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为y=x2-2x-3;
(2)设动点P的坐标为(m,m2-2m-3),
若足S△PAB=10,
则![]() AB×|m2-2m-3|=10,
AB×|m2-2m-3|=10,
即2|m2-2m-3|=10,
解得m=4或m=-2;
当m=4时,m2-2m-3=5,
当m=-2时,m2-2m-3=5,
综上P点的坐标为(-2,5)或(4,5);
(3)设点C关于对称轴的对称点为C′,连接AC′,直线AC′与对称轴的交点即为满足题意的Q点;
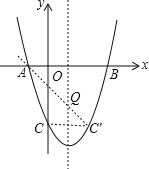
∵y=x2-2x-3=(x-1)2-4,
∴抛物线对称轴为x=1,C′坐标为(2,-3),
设直线AC′的解析式为y=kx+b,
根据题意可得![]() ,
,
解得![]() ,
,
所以直线AC′的解析式为y=-x-1,
当x=1时,y=-2,
即点Q的坐标为(1,-2).


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
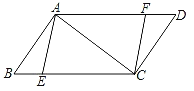
【题目】如图,在ABCD中,BC=10,对角线AC⊥AB,点EF在BC、AD上,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)当四边形AECF是菱形时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
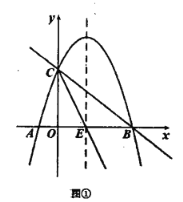
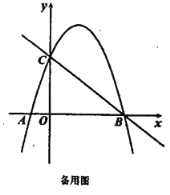
【题目】如图①,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,二次函数的对称轴与
,二次函数的对称轴与![]() 轴的交于点
轴的交于点![]() ,作射线
,作射线![]() .
.
![]() 抛物线
抛物线![]() 的解析式为 ; 点
的解析式为 ; 点![]() 坐标为_ ;
坐标为_ ;
![]() 求证:射线
求证:射线![]() 是
是![]() 的角平分线;
的角平分线;
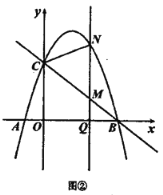
![]() 如图②,点
如图②,点![]() 是
是![]() 的正半轴上一点,过点
的正半轴上一点,过点![]() 作
作![]() 轴的平行线,与直线
轴的平行线,与直线![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,连结
,连结![]() ,将
,将![]() 沿
沿![]() 翻折,
翻折,![]() 的对应点为
的对应点为![]() .在图②中探究;是否存在点
.在图②中探究;是否存在点![]() ,使褥
,使褥![]() 恰好落在
恰好落在![]() 轴的正半轴上?若存在,请求出
轴的正半轴上?若存在,请求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有分别标有数字![]() 、
、![]() 、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
(1)从中任取一球,将球上的数字记为![]() ,求关于
,求关于![]() 的一元二次方程
的一元二次方程![]() 有实数根的概率;
有实数根的概率;
(2)从中任取一球,将球上的数字作为点的横坐标,记为![]() (不放回);再任取一球,将球上的数字作为点的纵坐标,记为
(不放回);再任取一球,将球上的数字作为点的纵坐标,记为![]() ,试用画树状图(或列表法)表示出点
,试用画树状图(或列表法)表示出点![]() 所有可能出现的结果,并求点
所有可能出现的结果,并求点![]() 落在第二象限内的概率.
落在第二象限内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
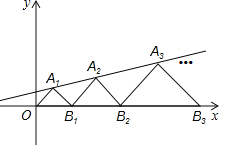
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() ,
,![]() ,…和
,…和![]() ,
,![]() ,
,![]() ,…分别在直线
,…分别在直线![]() 和
和![]() 轴上.
轴上.![]() ,
,![]() ,
,![]() ,…都是等腰直角三角形,它们的面积分别记作
,…都是等腰直角三角形,它们的面积分别记作![]() ,
,![]() ,
,![]() ,…,如果点
,…,如果点![]() 的坐标为
的坐标为![]() ,那么
,那么![]() 的纵坐标为_______.
的纵坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,我市某中学决定根据学生的兴趣爱好组建课外兴趣小组,因此学校随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)学校这次调查共抽取了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“戏曲”所在扇形的圆心角度数为 ;
(4)设该校共有学生2000名,请你估计该校有多少名学生喜欢书法?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解八年级500名学生的身体素质情况,体育老师从中随机抽取50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出如下频数分布表和频数分布直方图(不完整):
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 |
|
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
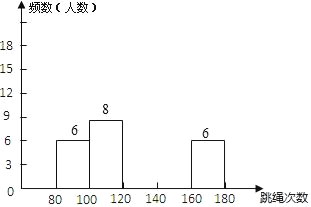
完成下列问题:
(1)请把上面的频数分布表和频数分布直方图补充完整;
(2)这个样本数据的中位数落在第 组;次数在140≤x<160这组的频率为 ;
(3)若八年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;x≥120合格,试问该年级合格的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
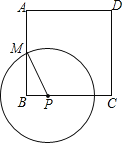
【题目】如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作![]() .当
.当![]() 与正方形ABCD的边相切时,BP的长为( )
与正方形ABCD的边相切时,BP的长为( )
A. 3B. ![]() C. 3或
C. 3或![]() D. 不确定
D. 不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com