
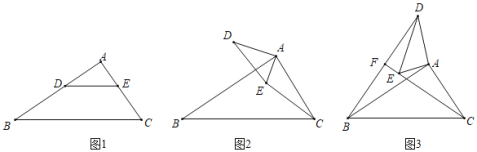
【题目】问题发现:
(1)如图1,在Rt△ABC中,∠A=90°,AB=kAC(k>1),D是AB上一点,DE∥BC,则BD,EC的数量关系为 .
类比探究
(2)如图2,将△AED绕着点A顺时针旋转,旋转角为a(0°<a<90°),连接CE,BD,请问(1)中BD,EC的数量关系还成立吗?说明理由
拓展延伸:
(3)如图3,在(2)的条件下,将△AED绕点A继续旋转,旋转角为a(a>90°).直线BD,CE交于F点,若AC=1,AB=![]() ,则当∠ACE=15°时,BFCF的值为_____.
,则当∠ACE=15°时,BFCF的值为_____.
【答案】(1)BD=kEC;(2)成立,理由见解析;(3)1或2.
【解析】
问题发现:(1)由平行线分线段成比例可得![]() ,即可得BD=kEC;
,即可得BD=kEC;
类比探究:(2)通过证明△ABD∽△ACE,可得![]() =k,即可得BD=kEC;
=k,即可得BD=kEC;
拓展延伸:(3)分两种情况讨论,由相似三角形的性质可得∠ACE=∠ABD,即可证∠BFC=90°,由直角三角形的性质和勾股定理可求BFCF的值.
问题发现:
(1)∵DE∥BC,
∴![]() ,
,![]()
∵AB=kAC,
∴BD=kEC,
故答案为:BD=kEC;
类比探究:
(2)成立,
理由如下:连接BD
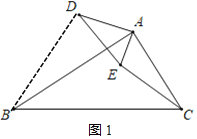
由旋转的性质可知,∠BAD=∠CAE
∵![]() ,
,
∴△ABD∽△ACE,
∴![]() =k,
=k,
故BD=kEC;
拓展延伸:
(3)BFCF的值为2或1;
由旋转的性质可知∠BAD=∠CAE
∵![]() ,
,
∴△ABD∽△ACE
∴∠ACE=15°=∠ABD
∵∠ABC+∠ACB=90°
∴∠FBC+∠FCB=90°
∴∠BFC=90°
∵∠BAC=90°,AC=1,AB=![]() ,
,
∴tan∠ABC=![]() ,
,
∴∠ABC=30°
∴∠ACB=60°
分两种情况
①如图2,
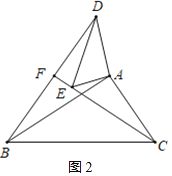
∴在Rt△BAC中,∠ABC=30°,AC=1,
∴BC=2AC=2,
∵在Rt△BFC中,∠CBF=30°+15°=45°,BC=2
∴BF=CF=![]()
∴BFCF=(![]() )2=2
)2=2
②如图3,
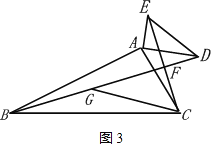
设CF=a,在BF上取点G
∵∠BCF=60°+15°=75°,∠CBF=∠ABC﹣∠ABD=30°﹣15°=15°,
∴∠CFB=90°
∴∠GCF=60°
∴CG=BG=2a,GF=![]() a.
a.
∵CF2+BF2=BC2
∴a2+(2a+![]() a) 2=22,
a) 2=22,
解得a2=2﹣![]() ,
,
∴BFCF=(2+![]() )aa=(2+
)aa=(2+![]() )a2=1,
)a2=1,
即:BFCF=1或2.
故答案为:1或2.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
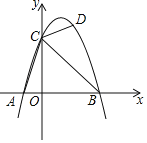
【题目】如图,已知二次函数y=﹣x2+2x+3的图象与x轴相交于点A,B,与y轴相交于点C,连接AC,BC.该函数在第一象限内的图象上是否存在一点D,使得CB平分∠ACD?若存在,求点D的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
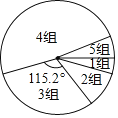
【题目】学习一定要讲究方法,比如有效的预习可大幅提高听课效率.九年级(1)班学习兴趣小组为了了解全校九年级学生的预习情况,对该校九年级学生每天的课前预习时间(单位:![]() )进行了抽样调查.并将抽查得到的数据分成5组,下面是未完成的频数、顿率分布表和频数分布扇形图.
)进行了抽样调查.并将抽查得到的数据分成5组,下面是未完成的频数、顿率分布表和频数分布扇形图.
组别 | 课前预习时间 | 频数(人数) | 频率 |
1 |
| 2 | |
2 |
|
| 0.10 |
3 |
| 16 | 0.32 |
4 |
|
|
|
5 |
| 3 |
请根据图表中的信息,回答下列问题:
(1)本次调查的样本容量为 ,表中的![]() ,
,![]() ,
,![]() ;
;
(2)试计算第4组人数所对应的扇形圆心角的度数;
(3)该校九年级其有1000名学生,请估计这些学生中每天课前预习时间不少于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
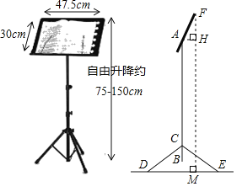
【题目】如图是小明同学的一款琴谱架,他由谱板、立杆和三角支架组成(立杆垂直于地面,三角支架的三条腿长相等),谱板的长为47.5cm,宽为30cm,在谱板长的中间,宽的下端![]() 处可调节谱板的倾斜度.如图是这款琴谱架的一种截面图.已知立杆AB=80cm,三角支架CD=30cm,CD与地面夹角∠CDE为35°,BC的长度为9cm.根据小明的身高,当谱板与水平面的夹角∠FAH调整为65°时,视谱效果最好,求此时谱板的上边沿到地面的距离FM的长.(结果精确到1cm.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin65°≈0.91,cos65°≈0.42,tan65°≈2.15)
处可调节谱板的倾斜度.如图是这款琴谱架的一种截面图.已知立杆AB=80cm,三角支架CD=30cm,CD与地面夹角∠CDE为35°,BC的长度为9cm.根据小明的身高,当谱板与水平面的夹角∠FAH调整为65°时,视谱效果最好,求此时谱板的上边沿到地面的距离FM的长.(结果精确到1cm.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin65°≈0.91,cos65°≈0.42,tan65°≈2.15)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了减少雾霾的侵状,某市环保局与市委各部门协商,要求市民在春节期间禁止燃放烟花爆竹,为了征集市民对禁燃的意见,政府办公室进行了抽样调查,调查意见表设计为:“满意““一般””无所谓””反对”四个选项,调查结果汇总制成如下不完整的统计图,请根据提供的信息解答下面的问题.
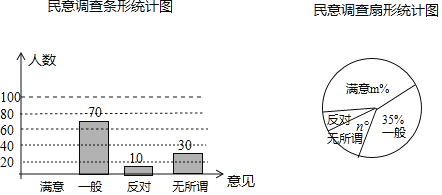
(1)参与问卷调查的人数为 .
(2)扇形统计图中的m= ,n= .补全条形统计图;
(3)若本市春节期间留守市区的市民有32000人,请你估计他们中持“反对”意见的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
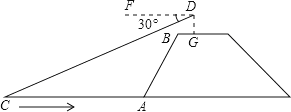
【题目】如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:![]() =1.73,结果保留两位有效数字)
=1.73,结果保留两位有效数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
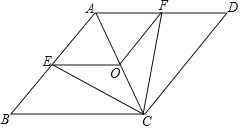
【题目】已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com