
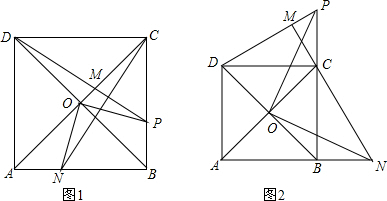
 �ڱ߳�Ϊ4��������ABCD�У���O�������ζԽ��ߵĽ��㣬����P������BC���˶�������C���߶�DP�Ĵ��ߣ����߶�DP�ڵ�M����ֱ��AB�ڵ�N������OP��ON������P���߶�BC���˶�ʱ����ͼ1��ʾ������P���߶�BC���ӳ������˶�ʱ����ͼ2��ʾ��
�ڱ߳�Ϊ4��������ABCD�У���O�������ζԽ��ߵĽ��㣬����P������BC���˶�������C���߶�DP�Ĵ��ߣ����߶�DP�ڵ�M����ֱ��AB�ڵ�N������OP��ON������P���߶�BC���˶�ʱ����ͼ1��ʾ������P���߶�BC���ӳ������˶�ʱ����ͼ2��ʾ������ ��1�����������ε����ʵó�DC=BC����DCB=��CBN=90�㣬�����CPD=��DCN=��CNB��֤��DCP�ա�CBN�����CP=BN��֤��OBN�ա�OCP���Ƴ�ON=OP����BON=��COP�������PON=��COB���ɣ�
��2��ͬ����֤ͼ2ʱ��OP=ON��OP��ON��ͼ1�У�S�ı���OPBN=S��OBN+S��BOP������������ɣ�ͼ2�У�S�ı���OBNP=S��POB+S��PBN������������ɣ�
��� ��1��֤�������ı���ABCDΪ�����Σ�
��OC=OB��DC=BC����DCB=��CBA=90�㣬��OCB=��OBA=45�㣬��DOC=90�㣬DC��AB��
��DP��CN��
���CMD=��DOC=90�㣬
���BCN+��CPD=90�㣬��PCN+��DCN=90�㣬
���CPD=��CNB��
��DC��AB��
���DCN=��CNB=��CPD��
���ڡ�DCP�͡�CBN��
$\left\{\begin{array}{l}{��DCB=��CBN}\\{��CPD=��BNC}\\{DC=BC}\end{array}\right.$��
���DCP�ա�CBN��AAS����
��CP=BN��
���ڡ�OBN�͡�OCP��
$\left\{\begin{array}{l}{OB=OC}\\{��OCP=��OBN}\\{CP=BN}\end{array}\right.$��
���OBN�ա�OCP��SAS����
��ON=OP����BON=��COP��
���BON+��BOP=��COP+��BOP��
����NOP=��BOC=90�㣬
��ON��OP��
��ON=OP��ON��OP��
��2���⣺��AB=4���ı���ABCD�������Σ�
��O��BC�ߵľ�����2��
ͼ1�У�S�ı���OPBN=S��OBN+S��BOP��
=$\frac{1}{2}$����4-x����2+$\frac{1}{2}$��x��2��
=4��0��x��4����
ͼ2�У�S�ı���OBNP=S��POB+S��PBN
=$\frac{1}{2}$��x��2+$\frac{1}{2}$����x-4����x
=$\frac{1}{2}$x2-x��x��4����
����O��P��B��NΪ������ı��ε����y��x�ĺ�����ϵ�ǣ�$\left\{\begin{array}{l}{y=4��0��x��4��}\\{y={\frac{1}{2}x}^{2}-x��x��4��}\end{array}\right.$��
���� ���⿼�������������ʣ�ȫ�������ε����ʺ��ж����ֶκ�����֪ʶ���Ӧ�ã��⣨1��С��Ĺؼ������������ʽ����������⣨2���Ĺؼ��������������������������������һ���Ĵ����ԣ���һ���ȽϺõ���Ŀ��ע�⣺֤���������ƣ�


 һ����������ϵ�д�
һ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��$\frac{1}{3}$ | B�� | x��$\frac{1}{3}$ | C�� | x��-$\frac{1}{3}$ | D�� | x��-$\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
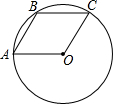 ��ͼ����O����?OABC�Ķ���A��B��C����OA=3����$\widehat{AB}$�ij�Ϊ�У���������У���
��ͼ����O����?OABC�Ķ���A��B��C����OA=3����$\widehat{AB}$�ij�Ϊ�У���������У����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
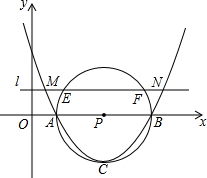 ��ͼ����֪������y=mx2-6mx+5m��x�ύ��A��B���㣬��ABΪֱ���ġ�P�����������ߵĶ���C��ֱ��l��x�ᣬ������������M��N���㣬����P��E��F���㣬��EF=2$\sqrt{3}$����MN�ij�Ϊ��������
��ͼ����֪������y=mx2-6mx+5m��x�ύ��A��B���㣬��ABΪֱ���ġ�P�����������ߵĶ���C��ֱ��l��x�ᣬ������������M��N���㣬����P��E��F���㣬��EF=2$\sqrt{3}$����MN�ij�Ϊ��������| A�� | 2$\sqrt{6}$ | B�� | 4$\sqrt{2}$ | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
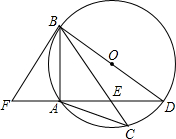 ��ͼ���ڡ�O�У�AB=AC��BDΪֱ������AD��BC�ཻ�ڵ�E���ӳ�DA��F��ʹ��ABF=��ABC��
��ͼ���ڡ�O�У�AB=AC��BDΪֱ������AD��BC�ཻ�ڵ�E���ӳ�DA��F��ʹ��ABF=��ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
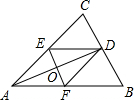 ��ͼ��AD�ǡ�CAB��ƽ���ߣ�DE��AB��DF��AC��EF��AD�ڵ�O�����ʣ�
��ͼ��AD�ǡ�CAB��ƽ���ߣ�DE��AB��DF��AC��EF��AD�ڵ�O�����ʣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
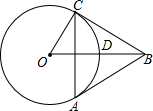 ��ͼ����O�İ뾶Ϊ2��OB=4��OB����O�ڵ�D����C�ǡ�O��һ���㣬��BCΪ���������ȱߡ�ABC��
��ͼ����O�İ뾶Ϊ2��OB=4��OB����O�ڵ�D����C�ǡ�O��һ���㣬��BCΪ���������ȱߡ�ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com