
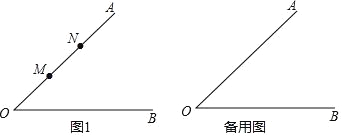
【题目】如图,∠AOB=45°,点M,N在边OA上,点P是边OB上的点.
(1)利用直尺和圆规在图1确定点P,使得PM=PN;
(2)设OM=x,ON=x+4,
①若x=0时,使P、M、N构成等腰三角形的点P有 个;
②若使P、M、N构成等腰三角形的点P恰好有三个,则x的值是____________.
【答案】(1)见解析;(2)①3;②:x=0或x=4![]() ﹣4或4<x<4
﹣4或4<x<4![]() ;
;
【解析】
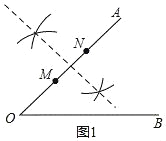
(1)分别以M、N为圆心,以大于![]() MN为半径作弧,两弧相交与两点,过两弧交
MN为半径作弧,两弧相交与两点,过两弧交
点的直线就是MN的垂直平分线;
(2)①分为PM=PN,MP=MN,NP=NM三种情况进行判断即可;②如图3,构建腰长为4
的等腰直角△OMC,和半径为4的⊙M,发现M在点D的位置时,满足条件;如图4,根
据等腰三角形三种情况的画法:分别以M、N为圆心,以MN为半径画弧,与OB的交点就
是满足条件的点P,再以MN为底边的等腰三角形,通过画图发现,无论x取何值,以MN
为底边的等腰三角形都存在一个,所以只要满足以MN为腰的三角形有两个即可.
(1)如图所示:
(2)①如图所示:
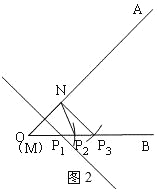
故答案为:3.
②如图3,以M为圆心,以4为半径画圆,当⊙M与OB相切时,设切点为C,⊙M与OA交于D,
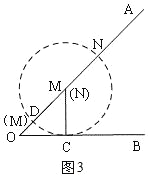
∴MC⊥OB,
∵∠AOB=45°,
∴△MCO是等腰直角三角形,
∴MC=OC=4,
∴![]()
当M与D重合时,即![]() 时,同理可知:点P恰好有三个;
时,同理可知:点P恰好有三个;
如图4,取OM=4,以M为圆心,以OM为半径画圆.
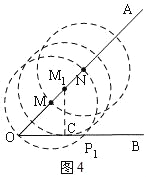
则⊙M与OB除了O外只有一个交点,此时x=4,即以∠PMN为顶角,MN为腰,符合条件的点P有一个,以N圆心,以MN为半径画圆,与直线OB相离,说明此时以∠PNM为顶角,以MN为腰,符合条件的点P不存在,还有一个是以NM为底边的符合条件的点P;
点M沿OA运动,到M1时,发现⊙M1与直线OB有一个交点;
∴当![]() 时,圆M在移动过程中,则会与OB除了O外有两个交点,满足点P恰好有三个;
时,圆M在移动过程中,则会与OB除了O外有两个交点,满足点P恰好有三个;
综上所述,若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是:x=0或![]() 或
或![]()
故答案为:x=0或![]() 或
或![]()


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】郑州市自2019年12月1日起推行垃圾分类,广大市民对垃圾桶的需求剧增.为满足市场需求,某超市花了7900元购进大小不同的两种垃圾桶共800个,其中,大桶和小桶的进价及售价如表所示.
大桶 | 小桶 | |
进价(元/个) | 18 | 5 |
售价(元/个) | 20 | 8 |
(1)该超市购进大桶和小桶各多少个?
(2)当小桶售出了300个后,商家决定将剩下的小桶的售价降低1元销售,并把其中一定数量的小桶作为赠品,在顾客购买大桶时,买一赠一(买一个大桶送一个小桶),送完即止.
请问:超市要使这批垃圾桶售完后获得的利润为1550元,那么小桶作为赠品送出多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题:
例题:已知二次三项式![]() 有一个因式是
有一个因式是![]() ,求另一个因式以及
,求另一个因式以及![]() 的值.
的值.
解:设另一个因式为![]() ,得
,得![]() ,
,
则![]() ,
,
![]() ,
,
解得,![]() ,
,
∴另一个因式为![]() ,
,![]() 的值为
的值为![]() .
.
仿照例题方法解答:
(1)若二次三项式![]() 的一个因式为
的一个因式为![]() ,求另一个因式;
,求另一个因式;
(2)若二次三项式![]() 有一个因式是
有一个因式是![]() ,求另一个因式以及
,求另一个因式以及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个工程队共同参与一项筑路工程,甲队单独施工3个月,这时增加了乙队,两队又共同工作了2个月,总工程全部完成,已知甲队单独完成全部工程比乙队单独完成全部工程多用2个月,设甲队单独完成全部工程需![]() 个月,则根据题意可列方程中错误的是( )
个月,则根据题意可列方程中错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展了“手机伴我健康行”主题活动.他们随机抽取部分学生进行“手机使用目的”和“每周使用手机时间”的问卷调查,并绘制成如图①②的统计图。已知“查资料”人人数是40人。

请你根据以上信息解答以下问题
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是_______________。
(2)补全条形统计图
(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车开往距离出发地![]() 的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前
的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前![]() 到达目的地,设前一个小时的行驶速度为
到达目的地,设前一个小时的行驶速度为![]()
(1)直接用![]() 的式子表示提速后走完剩余路程的时间为
的式子表示提速后走完剩余路程的时间为
(2)求汽车实际走完全程所花的时间.
(3)若汽车按原路返回,司机准备一半路程以![]() 的速度行驶,另一半路程以
的速度行驶,另一半路程以![]() 的速度行驶(
的速度行驶(![]() ),朋友提醒他一半时间以
),朋友提醒他一半时间以![]() 的速度行驶,另一半时间以
的速度行驶,另一半时间以![]() 的速度行驶更快,你觉得谁的方案更快?请说明理由.
的速度行驶更快,你觉得谁的方案更快?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的反比例函数,且当x=2时,y=﹣3,
(1)求y与x之间的函数关系式;
(2)画出这个函数的图象;
(3)试判断点P(﹣2,3)是否在这个函数的图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com