
【题目】已知一次函数![]() 和
和![]() .
.
(1)在同一直角坐标系内,画出这两个函数的大致图象;

(2)直接写出:①函数![]() 与坐标轴围成的图形的面积为_______;
与坐标轴围成的图形的面积为_______;
②函数![]() 与坐标轴围成的图形的面积为________;
与坐标轴围成的图形的面积为________;
③这两个函数图象与![]() 轴围成的图形的面积为_________.
轴围成的图形的面积为_________.
(3)若反比例函数![]() 经过这两个函数图象的交点,则k的值为______.
经过这两个函数图象的交点,则k的值为______.
【答案】(1)画出这两个函数的大致图象见解析;(2)① ![]() ;②
;② ![]() ;③
;③ ![]() ;(3)3.
;(3)3.
【解析】
(1)把x=0,x=-1分别代入![]() 得出y值,描出两点,作出过两点的直线即可得
得出y值,描出两点,作出过两点的直线即可得![]() 的图象;把x=-1,x=-2分别代入
的图象;把x=-1,x=-2分别代入![]() 得出y值,描出两点,作出过两点的直线即可得
得出y值,描出两点,作出过两点的直线即可得![]() 的图象;
的图象;
(2)①分别令x=0,y=0,可分别求出x、y的值,根据直线与坐标轴围成的图形的面积=![]() |x||y|即可得答案;
|x||y|即可得答案;
②分别令x=0,y=0,可分别求出x、y的值,根据直线与坐标轴围成的图形的面积=![]() |x||y|即可得答案;
|x||y|即可得答案;
③由①②可知两直线与x轴的交点坐标,联立两直线解析式,解方程组可求出两直线的交点坐标,即可求出两个函数图象与![]() 轴围成的图形的面积;
轴围成的图形的面积;
(3)把两图象的交点坐标代入反比例函数解析式可求出k值,即可得答案.
(1)当x=0时,![]() =1,当x=-1时,
=1,当x=-1时,![]() =-3,
=-3,
当x=-1时,![]() =-3,当x=-2时,
=-3,当x=-2时,![]() =-1,
=-1,
∴两个函数的大致图象如图所示:
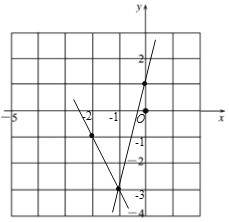
(2)①当x=0时,y=4x+1=1,
当y=0时,4x+1=0,
解得:x=![]() ,
,
∴函数![]() 与坐标轴围成的图形的面积为
与坐标轴围成的图形的面积为![]() ×|
×|![]() |×|1|=
|×|1|=![]() ,
,
故答案为:![]()
②当x=0时,y=-2x-5=-5,
当y=0时,-2x-5=0,
解得:x=![]() ,
,
∴函数y=-2x-5与坐标轴围成的图形的面积为![]() ×|
×|![]() |×|-5|=
|×|-5|=![]() ,
,
故答案为:![]()
③联立两直线解析式得:![]() ,
,
解得:![]() ,
,
∴两直线的交点坐标为(-1,-3),
由①②可知两直线与x轴当交点坐标为(![]() ,0)和(
,0)和(![]() ,0),
,0),
∴两个函数图象与![]() 轴围成的图形的面积为
轴围成的图形的面积为![]() ×|
×|![]() -(
-(![]() )|×|-3|=
)|×|-3|=![]() ,
,
故答案为:![]()
(3)∵两直线的交点坐标为(-1,-3),
∴k=(-1)×(-3)=3,
故答案为:3


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图是某一蓄水池每1h的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数图象。
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出函数的函数表达式;
(3)若要6h排完水池的水,那么每1h的排水量应该是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,回答问题:
解方程x4-5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2-5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;
当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=-1,x3=2,x4=-2.
在由原方程得到方程①的过程中,利用换元法达到降次的目的,体现了数学的转化思想,请利用上述方法解方程
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() .
.
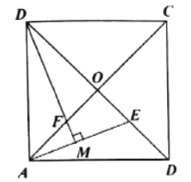
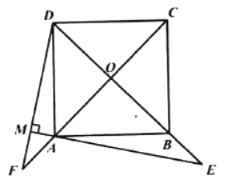
(1) (2)
(1)若点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .求证:
.求证:![]() ;
;
(2)若点![]() 在
在![]() 的延长线上,
的延长线上,![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,其他条件不变结论“
,其他条件不变结论“![]() ”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲和乙骑摩托车分别从某大道上相距6000米的A、B两地同时出发,相向而行,匀速行驶一段时间后,到达C地的甲发现摩托车出了故障,立即停下电话通知乙,乙接到电话后立即以出发时速度的![]() 倍向C地匀速骑行,到达C地后,用5分钟修好了甲摩托车,然后乙仍以出发时速度的
倍向C地匀速骑行,到达C地后,用5分钟修好了甲摩托车,然后乙仍以出发时速度的![]() 倍匀速向终点A地骑行,甲仍以原来速度向B地匀速骑行,2分钟后,发现乙的一件维修工具落在了自己车上,于是立即掉头并以原速度
倍匀速向终点A地骑行,甲仍以原来速度向B地匀速骑行,2分钟后,发现乙的一件维修工具落在了自己车上,于是立即掉头并以原速度![]() 倍的速度匀速返回(此时乙未到达A地).在这个过程中,两人相距的路程y(米)与甲出发的时间x(分)之间的关系如图所示(甲与乙打、接电话及掉头时间忽略不计)则当乙到达A地时,甲离A地的距离为 ________米.
倍的速度匀速返回(此时乙未到达A地).在这个过程中,两人相距的路程y(米)与甲出发的时间x(分)之间的关系如图所示(甲与乙打、接电话及掉头时间忽略不计)则当乙到达A地时,甲离A地的距离为 ________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④![]() 。其中正确的结论有( )
。其中正确的结论有( )
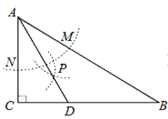
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 延长线上任意一点,以
延长线上任意一点,以![]() 为直角边作等腰直角
为直角边作等腰直角![]() ,且
,且![]() ,连结
,连结![]() .
.
(![]() )求证:
)求证: ![]() .
.
(![]() )在点
)在点![]() 运动过程中,试问
运动过程中,试问![]() 的度数是否会变化?若不变,请求出它的度数,若变化,请说明它的变化趋势.
的度数是否会变化?若不变,请求出它的度数,若变化,请说明它的变化趋势.
(![]() )已知
)已知![]() ,设
,设![]() ,
, ![]() .
.
①试求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
②当![]() 时,求
时,求![]() 的外接圆半径.
的外接圆半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com