
分析 等量关系为:(每件的售价-每件的进价)×[原来卖出的数量-20×(超过50元的售价÷2)]=8000,把相关数值代入求得正数解即为售价的相应值.
解答 解:设售价应定为x元.
(x-40)[500-$\frac{x-50}{2}$×20]=8000.
解得:x1=60,x2=80.
此时的销售量为:500-(60-50)×10=400(件),
500-(80-50)×10=200(件),
故进货量应为400或200件.
答:售价为60或80元,进货量应为400件或200件.
点评 此题主要考查了一元二次方程的应用;得到提高价格后的销售量是解决本题的难点;得到总利润的等量关系是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.708×10-6米 | B. | 7.08×10-7米 | C. | 70.8×10-8米 | D. | 708×10-9米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
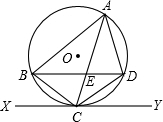 如图,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,弦BD∥XY,AC,BD相交于点E.
如图,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,弦BD∥XY,AC,BD相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,AB,CD相交于点E,CF,BF分别为∠ACD和∠ABD的平分线且相交于点F,求证:∠F=$\frac{1}{2}$(∠A+∠D).
如图所示,AB,CD相交于点E,CF,BF分别为∠ACD和∠ABD的平分线且相交于点F,求证:∠F=$\frac{1}{2}$(∠A+∠D).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com