
【题目】如图.在![]() 中,
中,![]() ,
,![]() ,
,![]() , 动点
, 动点![]() 从点
从点![]() 出发以每秒3个单位的速度运动至点
出发以每秒3个单位的速度运动至点![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒
秒![]() .
.
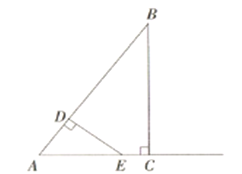
(1)线段![]() 长为 .(用含
长为 .(用含![]() 的代数式表示)
的代数式表示)
(2)若![]() 与
与![]() 的面积比为1:4时, 求
的面积比为1:4时, 求![]() 的值.
的值.
(3)设![]() 与
与![]() 重叠部分图形的周长为
重叠部分图形的周长为![]() , 求
, 求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当直线![]() 把
把![]() 分成的两部分图形中有一个是轴对称图形时,直接写出
分成的两部分图形中有一个是轴对称图形时,直接写出![]() 的值.
的值.
【答案】(1)5t;(2)t=1;(3)当![]() 时,
时,![]() ;当
;当![]() 时,
时, ![]() ;(4)
;(4)![]() 或t=2
或t=2
【解析】
(1)先在Rt△ABC中求出tanA,再在Rt△ADE中求出DE,最后利用勾股定理求出AE;
(2)先判断出△ABC∽△AED,再根据面积比得出相似比,进而列式计算即可;
(3)由(1)(2)得:AD=3t,DE=4t,AE=5t,BD=103t,△ABC∽△AED,然后分情况讨论:当0<t≤![]() 时;当
时;当![]() 时;分别利用相似三角形的性质求出重叠部分图形的边长,然后计算周长;
时;分别利用相似三角形的性质求出重叠部分图形的边长,然后计算周长;
(4)分两种情况:当E在线段AC上,DE=CE时,四边形BCED是轴对称图形;当DE和BC相交于F,AD=AC时,四边形ACFD是轴对称图形;分别用相等的线段建立方程求解即可.
解:(1)由题意得,AD=3t,
在Rt△ABC中,![]() ,
,
在Rt△ADE中,![]() ,
,
∴DE=4t,
根据勾股定理得,AE=5t,
故答案为:5t;
(2)∵ED⊥AB,∠ACB=90°,
∴∠ACB=∠ADE=90°,
∵∠A=∠A,
∴△ABC∽△AED,
∵![]() 与
与![]() 的面积比为1:4,
的面积比为1:4,
∴![]() ,即
,即![]() ,
,
∴t=1;
(3)由(1)(2)得:AD=3t,DE=4t,AE=5t,△ABC∽△AED,
∵![]() ,
,
∴BD=103t,
当E、C重合时,即5t=6,
解得:![]() ,
,
∴当0<t≤![]() 时,L=3t+4t+5t=12t;
时,L=3t+4t+5t=12t;
当D、B重合时,即3t=10,
解得:![]() ,
,
∴当![]() 时,如图,
时,如图,
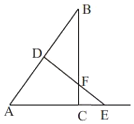
∵∠B=∠B,∠BDF=∠BCA,
∴△ABC∽△FBD,
∴![]() ,即
,即![]() ,
,
∴DF=![]() ,
,
∵∠BFD=∠EFC,∠BDF=∠ECF,
∴∠B=∠E,
∵∠FCE=∠BCA,
∴△BCA∽△ECF,
∴![]() ,即
,即![]() ,
,
∴CF=![]() ,
,
∴![]() ,
,
综上:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
(4)当E在线段AC上,DE=CE时,四边形BCED是轴对称图形,
由(1)知,AE=5t,DE=4t,
∴CE=65t,
∴4t=65t,
解得:![]() ,
,
当DE和BC相交于F,AD=AC时,四边形ACFD是轴对称图形,
∵AD=3t,AC=6,
∴3t=6,
解得:t=2,
故t的值为![]() 或2.
或2.



 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】清朝数学家梅文鼎的著作《方程论》中有这样一道题:山田三亩,场地六亩,共折实田四亩七分;又山田五亩,场地三亩,共折实田五亩五分,问每亩山田折实田多少,
每亩场地折实田多少?
译文为:假如有山田3亩,场地6亩,其产粮相当于实田4.7亩;又山田5亩,场地3亩,其产粮相当于实田5.5亩,问每亩山田和每亩场地产粮各相当于实田多少亩?请你解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
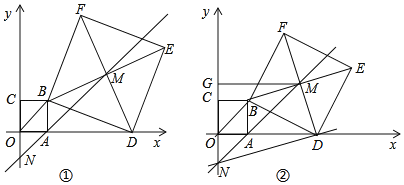
【题目】如图①,在直角坐标系中,点A的坐标为(1,0),以OA为边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
(1)试找出图1中的一个损矩形;
(2)试说明(1)中找出的损矩形的四个顶点一定在同一个圆上;
(3)随着点D位置的变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由;
(4)在图②中,过点M作MG⊥y轴于点G,连接DN,若四边形DMGN为损矩形,求D点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:

(1)方程ax2+bx+c=0的两个根为____________;
(2)不等式ax2+bx+c>0的解集为________;
(3)y随x的增大而减小的自变量x的取值范围为________;
(4)若方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
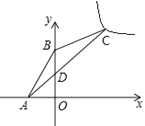
【题目】如图,在平面直角坐标系![]() 中,点A(
中,点A(![]() ,0),B(0,2),点C在第一象限,∠ABC=135°,AC交
,0),B(0,2),点C在第一象限,∠ABC=135°,AC交![]() 轴于D,CD=3AD,反比例函数
轴于D,CD=3AD,反比例函数![]() 的图象经过点C,则
的图象经过点C,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具专柜从太原市小商品批发市场购进一批胶带,每个进价0.5元.调查发现,当销售价为0.8元时,每月可售出500个;如果售价每降低0.05元,那么平均每月可多售出200个.
(1)当降价0.2元时,平均每月销售胶带______个;
(2)摊主要想平均每月赢利180元,且尽可能让利与顾客,应该如何定价?
(3)在(2)的条件下,每个胶带的利润率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,对称轴分别交抛物线和
,对称轴分别交抛物线和![]() 轴于点
轴于点![]() 和点
和点![]() ,以
,以![]() 为底边向上作等腰
为底边向上作等腰![]() .
.
(1)![]() ______;
______;![]() ______(用含
______(用含![]() 的代数式表示);
的代数式表示);
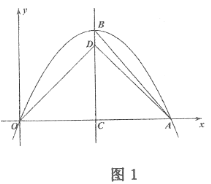
(2)如图1,当![]() 时,连接
时,连接![]() ,求
,求![]() 的值;
的值;
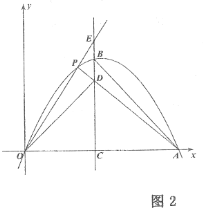
(3)点![]() 是抛物线
是抛物线![]() 段上任意一点,连接
段上任意一点,连接![]() 和
和![]() ,延长
,延长![]() 交对称轴于点
交对称轴于点![]() ,如图2,若
,如图2,若![]() ,
,![]() ,
,![]() 三点在一条直线上,当
三点在一条直线上,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
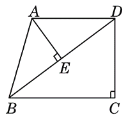
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠C=90°,AB=AD,连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)若 AD=25,BC=32,求线段AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com