
【题目】已知![]() 过点(2,-1),与
过点(2,-1),与![]() 轴交于点A,F点为(1,2).
轴交于点A,F点为(1,2).
(Ⅰ)求![]() 的值及A点的坐标;
的值及A点的坐标;
(Ⅱ)将函数![]() 的图象沿
的图象沿![]() 轴方向向上平移得到函数
轴方向向上平移得到函数![]() ,其图象与
,其图象与![]() 轴交于点Q,且OQ=QF,求平移后的函数
轴交于点Q,且OQ=QF,求平移后的函数![]() 的解析式;
的解析式;
(Ⅲ)若点A关于![]() 的对称点为K,请求出直线FK与
的对称点为K,请求出直线FK与![]() 轴的交点坐标.
轴的交点坐标.
【答案】(Ⅰ) k=-1,A(1,0);(Ⅱ)见解析;(Ⅲ)y=-7x+9;(![]() ,0).
,0).
【解析】
(Ⅰ)将(2,-1)代入直线解析式中,求出k,即可得出结论;
(Ⅱ)构造直角三角形,利用勾股定理求出点Q的坐标,即可得出结论;
(Ⅲ)先确定出点D,Q的坐标,即可判断出∠ODQ=45°,进而求出点K的坐标,即可得出结论.
(Ⅰ)∵y1=kx+1经过点(2,-1),
∴2k+1=-1,
∴k=-1,y1=-x+1,
令y=0,
∴x=1,
∴A(1,0);
(Ⅱ)设平移后的直线解析式为y=-x+m,
∴Q(0,m),
如图,过点F作EF⊥y轴于E,
∵F点为(1,2),
∴EF=1,EQ=2-m,FQ=OQ=m,
根据勾股定理得,EF2+EQ2=FQ2,
∴1+(2-m)2=m2,
∴m=![]() ,
,
∴平移后的函数y2的解析式y2=x+![]() ;
;
③如图,设直线y2=x+![]() 与x轴的交点为D,
与x轴的交点为D,
∴D(![]() ,0),Q(0,
,0),Q(0,![]() ),
),
∴OD=OQ,
∴∠ODQ=45°,
∵A(1,0),
∴AD=ODOA=![]() ,
,
连接DH,
∵点A关于y1的对称点为K,
∴DK=DA=![]() ,∠KDQ=∠ODQ=45°,
,∠KDQ=∠ODQ=45°,
∴∠ADK=90°,
∴K(![]() ,
,![]() ),
),
∵F(1,2),
∴直线FK的解析式为y=7x+9,
∴FK与x轴的交点为(![]() ,0).
,0).


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图1,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上(点A与点B不重合),我们定义:这样的两条抛物L1 , L2互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条.
(1)如图2,已知抛物线L3:y=2x2﹣8x+4与y轴交于点C,试求出点C关于该抛物线对称轴对称的点D的坐标;
(2)请求出以点D为顶点的L3的友好抛物线L4的解析式,并指出L3与L4中y同时随x增大而增大的自变量的取值范围;
(3)若抛物y=a1 (x﹣m)2+n的任意一条友好抛物线的解析式为y=a2 (x﹣h)2+k,请写出a1与a2的关系式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=2x+1与双曲线y= ![]() 的一个交点为A(m,﹣3).
的一个交点为A(m,﹣3).
(1)求双曲线的表达式;
(2)过动点P(n,0)(n<0)且垂直于x轴的直线与直线y=2x+1和双曲线y= ![]() 的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
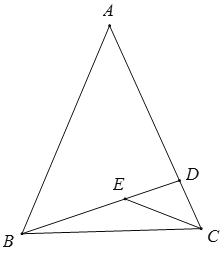
【题目】如图,在△ABC中,BD⊥AC于D.若∠A:∠ABC:∠ACB=3:4:5,E为线段BD上任一点.
(1)试求∠ABD的度数;
(2)求证:∠BEC>∠A.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
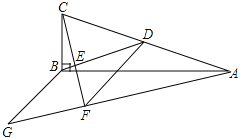
【题目】在![]() 中,
中,![]() ,BD为AC边上的中线,过点C作
,BD为AC边上的中线,过点C作![]() 于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取
于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取![]() ,连接BG,DF.
,连接BG,DF.
![]() 求证:
求证:![]() ;
;
![]() 求证:四边形BDFG为菱形;
求证:四边形BDFG为菱形;
![]() 若
若![]() ,
,![]() ,求四边形BDFG的周长.
,求四边形BDFG的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com