
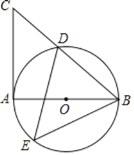
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,
,![]() 是
是![]() 上一点,且与点
上一点,且与点![]() 在
在![]() 异侧,连结
异侧,连结![]()
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,则
,则![]() 的长为(结果保留
的长为(结果保留![]() )
)
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图:已知![]() ,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程_____.
,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB 为圆O的直径, PQ切圆O于T , AC⊥PQ于C ,交圆O于 D .
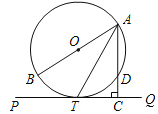
(1)求证: AT 平分∠BAC ;
(2)若 AD =2 , TC=![]() ,求圆O的半径.
,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
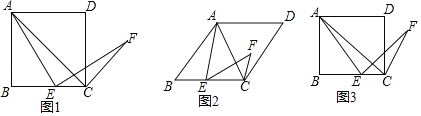
【题目】由特殊到一般、类比、转化是数学学习和研究中经常用到的思想方法.下面是对一道几何题进行变式探究的思路,请你运用上述思想方法完成探究任务.问题情境:在四边形ABCD中,AC是对角线,E为边BC上一点,连接AE.以E为旋转中心,将线段AE顺时针旋转,旋转角与∠B相等,得到线段EF,连接CF.
(1)特例如图1,若四边形ABCD是正方形,求证:AC⊥CF;
(2)拓展分析一:如图2,若四边形ABCD是菱形,探究下列问题:
①当∠B=50°时,求∠ACF的度数;
②针对图2的条件,写出一般的结论(不必证明);
(3)拓展探究二:如图3,若四边形ABCD是矩形,且BC=kAB(k>1).若前提条件不变,特例分析中得到的结论还成立吗?若成立,请证明;若不成立,修改题中的条件使结论成立(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx+c的图象经过(﹣1,0),对称轴x=1,则下列三个结论:①abc<0;②10a+3b+c>0;③am2+bm+a≥0.正确的结论为_____(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈尔滨某中学学校为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类).根据图中提供的信息,解答下面的问题:

(1)在这次调查中,参与问卷调查的学生共有多少名学生?
(2)通过计算补全条形统计图;
(3)若学校有900名学生,估计喜欢篮球和足球的学生共有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线y=x2﹣3x﹣4与x轴交于A,B两点(点A在点B的右侧),有点C(﹣2,6).
(1)求A,B两点的坐标.
(2)若点D(1,﹣3),点E在线段OA上,且∠ACB=∠ADE,延长ED交y轴于点F,求△EFO的面积.
(3)若M在直线AC上,点Q在抛物线上,是否存在点M和点N,使以Q,M,N,A为顶点的四边形是正方形?若存在,直接写出M点的坐标.若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
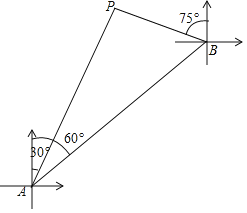
【题目】如图,一艘轮船在A处测得灯塔P在船的北偏东30°方向,轮船沿着北偏东60°方向航行16km后到达B处,这时灯塔P在船的北偏西75°方向.则灯塔P与B之间的距离等于___________km(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com