
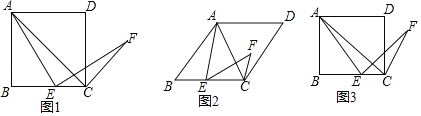
【题目】由特殊到一般、类比、转化是数学学习和研究中经常用到的思想方法.下面是对一道几何题进行变式探究的思路,请你运用上述思想方法完成探究任务.问题情境:在四边形ABCD中,AC是对角线,E为边BC上一点,连接AE.以E为旋转中心,将线段AE顺时针旋转,旋转角与∠B相等,得到线段EF,连接CF.
(1)特例如图1,若四边形ABCD是正方形,求证:AC⊥CF;
(2)拓展分析一:如图2,若四边形ABCD是菱形,探究下列问题:
①当∠B=50°时,求∠ACF的度数;
②针对图2的条件,写出一般的结论(不必证明);
(3)拓展探究二:如图3,若四边形ABCD是矩形,且BC=kAB(k>1).若前提条件不变,特例分析中得到的结论还成立吗?若成立,请证明;若不成立,修改题中的条件使结论成立(不必证明).
【答案】(1)见解析;(2)①50°;②∠ACF=∠B;(3)不成立,当EF=kAE时,AC⊥CF.
【解析】
(1)如图1中,作EH∥AC交AB于H.只要证明△HAE≌△CEF,即可推出∠AHE=∠ECF=135°,由∠BCA=45°,推出∠ACF=90°即可;
(2)①如图2中,作EH∥AC交AB于H.只要证明△HAE≌△CEF,即可解决问题.②同①中的证明方法可得∠ACF=∠B;
(3)结论:当EF=kAE时,AC⊥CF.如图3中,作EH∥AC交AB于H,AC与EF交于点O.只要证明△HAE∽△CEF,推出∠HEA=∠F,由∠HEA=∠CAE,推出∠CAE=∠F,由∠AOE=∠FOC,∠EAO+∠AOE=90°,推出∠FOC+∠F=90°,即可得到∠OCF=90°.
(1)证明:如图1中,作EH∥AC交AB于H.
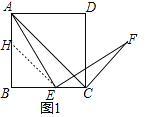
∵四边形ABCD是正方形,
∴AB=BC,∠BAC=∠BCA=45°,
∵EH∥AC,
∴∠BHE=∠BAC=45°,∠BEH=∠BCA=45°,
∴∠BHE=∠BEH=45°,∠AHE=135°,
∴BH=BE,
∴AH=CE,
∵∠AEC=∠B+∠BAE=∠AEF+∠CEF,∠AEF=∠B=90°,
∴∠HAE=∠CEF,
在△HAE和△CEF中,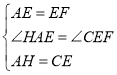 ,
,
∴△HAE≌△CEF(SAS),
∴∠AHE=∠ECF=135°,
∵∠BCA=45°,
∴∠ACF=90°,
∴AC⊥CF;
(2)解:①如图2中,作EH∥AC交AB于H.
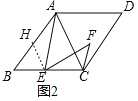
∵四边形ABCD是菱形,
∴AB=BC,∠BAC=∠BCA,
∵EH∥AC,
∴∠BHE=∠BAC,∠BEH=∠BCA,
∴∠BHE=∠BEH,
∴BH=BE,
∴AH=CE,
∵∠AEC=∠B+∠BAE=∠AEF+∠CEF,∠AEF=∠B,
∴∠HAE=∠CEF,
在△HAE和△CEF中,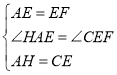 ,
,
∴△HAE≌△CEF(SAS),
∴∠AHE=∠ECF,
∵∠B=50°,
∴∠BHE=∠ACB=65°,
∴∠AHE=∠ECF=115°
∴∠ACF=115°﹣65°=50°;
②结论:∠ACF=∠B.证明如下:
同①可得△HAE≌△CEF,
∴∠AHE=∠ECF.
∴∠B+∠BEH=∠ACF+∠ACB,
又由①知∠BEH=∠ACB,
∴∠ACF=∠B;
(3)解:不成立,当EF=kAE时,AC⊥CF.理由如下:
如图3中,作EH∥AC交AB于H,AC与EF交于点O.
∵EH∥AC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∵EF=kAE,
∴![]() =
=![]() =
=![]() ,
,
∵∠AEC=∠B+∠BAE=∠AEF+∠CEF,∠AEF=∠B=90°,
∴∠HAE=∠CEF,

∴△HAE∽△CEF,
∴∠HEA=∠F,
∵∠HEA=∠CAE,
∴∠CAE=∠F,
∵∠AOE=∠FOC,∠EAO+∠AOE=90°,
∴∠FOC+∠F=90°,
∴∠OCF=90°,
∴AC⊥CF.


科目:初中数学 来源: 题型:
【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量是售价的一次函数,且相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是( )元;
(2)求月销量y与售价x的一次函数关系式:
(3)设销售该运动服的月利润为W元,那么售价为多少元时,当月的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的两直角边
的两直角边![]() ,
,![]() 分别在
分别在![]() 轴的负半轴和
轴的负半轴和![]() 轴的正半轴上,
轴的正半轴上,![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() 、
、![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,且顶点在直线
,且顶点在直线![]() 上.
上.
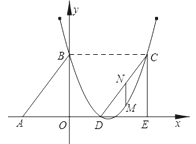
(1)求抛物线对应的函数关系式;
(2)若![]() 是由
是由![]() 沿
沿![]() 轴向右平移得到的,当四边形
轴向右平移得到的,当四边形![]() 是菱形时,试判断点
是菱形时,试判断点![]() 和点
和点![]() 是否在该抛物线上,并说明理由;
是否在该抛物线上,并说明理由;
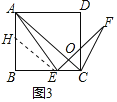
(3)在(2)的条件下,若![]() 点是
点是![]() 所在直线下方抛物线上的一个动点,过点
所在直线下方抛物线上的一个动点,过点![]() 作
作![]() 平行于
平行于![]() 轴交
轴交![]() 于
于![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的长度为
的长度为![]() .求
.求![]() 与
与![]() 之间的函数关系式,写出自变量
之间的函数关系式,写出自变量![]() 的取值范围,并求
的取值范围,并求![]() 取最大值时,点
取最大值时,点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),交
的左边),交![]() 轴正半轴于点
轴正半轴于点![]() .
.
(1)如图1,当![]() 时.
时.
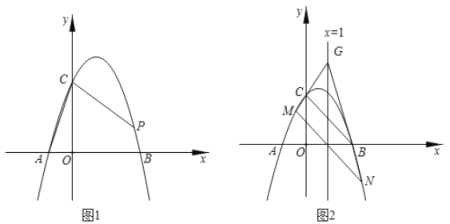
①直接写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
②若抛物线上有一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
(2)如图2,平移直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 在定直线
在定直线![]() 上运动,求
上运动,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
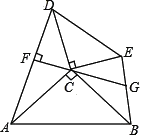
【题目】如图,点 C 为 Rt△ACB 与 Rt△DCE 的公共点,∠ACB=∠DCE=90°,连 接 AD、BE,过点 C 作 CF⊥AD 于点 F,延长 FC 交 BE 于点 G.若 AC=BC=25,CE=15, DC=20,则![]() 的值为___________.
的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,![]() ,BE是AC边上的中线,点D在射线BC上.
,BE是AC边上的中线,点D在射线BC上.
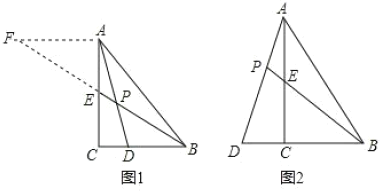
(1)如图1,点D在BC边上,![]() ,AD与BE相交于点P,过点A作
,AD与BE相交于点P,过点A作![]() ,交BE的延长线于点F,易得
,交BE的延长线于点F,易得![]() 的值为 ;
的值为 ;
(2)如图2,在△ABC中,![]() ,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,
,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若CD=2,AC=6,则BP= .
查看答案和解析>>
科目:初中数学 来源: 题型:
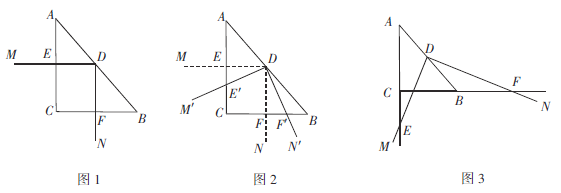
【题目】在△ABC中,![]() ,AC=4,BC=3,点D是斜边AB的中点. 以点D为顶点作
,AC=4,BC=3,点D是斜边AB的中点. 以点D为顶点作![]() ,射线DM、DN分别交边AC、CB于点E、F.
,射线DM、DN分别交边AC、CB于点E、F.
特例
(1)如图1,若![]() ,不添加辅助线,图1中所有与△ABC相似的三角形为 ,
,不添加辅助线,图1中所有与△ABC相似的三角形为 ,![]() ;
;
操作探究:
(2)将(1)中的![]() 从图1 的位置开始绕点D按逆时针方向旋转,得到
从图1 的位置开始绕点D按逆时针方向旋转,得到![]() .如图2,当射线
.如图2,当射线![]() 分别交边
分别交边![]() 于点
于点![]() 时,求
时,求![]() 的值;
的值;
拓展延伸:
(3)如图3,![]() 中,
中,![]() ,AC=m,BC=n,点D是斜边AB的中点,以点D为顶点作
,AC=m,BC=n,点D是斜边AB的中点,以点D为顶点作![]() ,射线
,射线![]() 分别交边
分别交边![]() 的延长线于点
的延长线于点![]() ,则
,则![]() 的值为_______________.(用含
的值为_______________.(用含![]() 的代数式表示,直接回答即可)
的代数式表示,直接回答即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com