
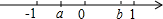 表示实数a,b的点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+|b-a|.
表示实数a,b的点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+|b-a|.  能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
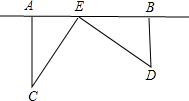 为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.0km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.0km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
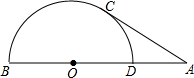 如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )
如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com