
分析 (1)设y=kx,当x=2时,y=3时,代入可得k,可得解析式;
(2)将点(3,2)和点(-2,1)的坐标代入解析式可得k,易得一次函数解析式.
解答 解:(1)∵y与x成正比例,
∴设y=kx,
∵当x=2时,y=3,
∴3=2k,
∴k=$\frac{3}{2}$,
∴正比例函数的解析式为:y=$\frac{3}{2}$x;
(2)∵直线y=kx+b经过点(3,2)和点(-2,1),
∴$\left\{\begin{array}{l}{2=3k+b}\\{1=-2k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{5}}\\{b=\frac{7}{5}}\end{array}\right.$,
∴解析式为:y=$\frac{1}{5}x+\frac{7}{5}$.
点评 本题主要考查了待定系数法求解析式,将坐标代入解得k,b是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
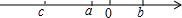 实数a、b、c在数轴上的位置如图所示,则$\sqrt{(a-b)^{2}}$-|a+c|+$\sqrt{(c-b)^{2}}$-|-b|=b.
实数a、b、c在数轴上的位置如图所示,则$\sqrt{(a-b)^{2}}$-|a+c|+$\sqrt{(c-b)^{2}}$-|-b|=b.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
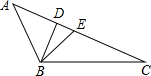 喜羊羊、美羊羊、懒羊羊在微信建立了一个学习讨论组,现在他们讨论了一道几何题,如图所示,请你填写完整的解答过程.
喜羊羊、美羊羊、懒羊羊在微信建立了一个学习讨论组,现在他们讨论了一道几何题,如图所示,请你填写完整的解答过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
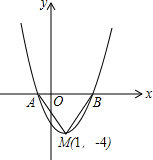 如图是二次函数y=(x-1)2-4的图象,与x轴交于A,B两点.将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.
如图是二次函数y=(x-1)2-4的图象,与x轴交于A,B两点.将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com