
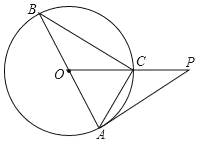
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,⊙O的切线AP与OC的延长线相交于点P,∠P=∠BCO.
(1)求证:AC=PC;
(2)若AB=6![]() ,求AP的长.
,求AP的长.
科目:初中数学 来源: 题型:
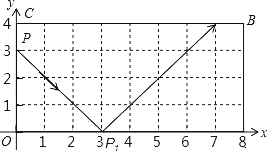
【题目】如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2的坐标是_____,点P2017的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
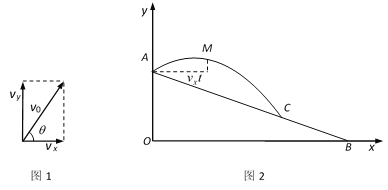
【题目】如图1,已知水龙头喷水的初始速度v0可以分解为横向初始速度vx和纵向初始速度vy,θ是水龙头的仰角,且![]() .图2是一个建在斜坡上的花圃场地的截面示意图,水龙头的喷射点A在山坡的坡顶上(喷射点离地面高度忽略不计),坡顶的铅直高度OA为15米,山坡的坡比为
.图2是一个建在斜坡上的花圃场地的截面示意图,水龙头的喷射点A在山坡的坡顶上(喷射点离地面高度忽略不计),坡顶的铅直高度OA为15米,山坡的坡比为![]() .离开水龙头后的水(看成点)获得初始速度v0米/秒后的运动路径可以看作是抛物线,点M是运动过程中的某一位置.忽略空气阻力,实验表明:M与A的高度之差d(米)与喷出时间t(秒)的关系为
.离开水龙头后的水(看成点)获得初始速度v0米/秒后的运动路径可以看作是抛物线,点M是运动过程中的某一位置.忽略空气阻力,实验表明:M与A的高度之差d(米)与喷出时间t(秒)的关系为![]() ;M与A的水平距离为
;M与A的水平距离为![]() 米.已知该水流的初始速度
米.已知该水流的初始速度![]() 为15米/秒,水龙头的仰角θ为
为15米/秒,水龙头的仰角θ为![]() .
.
(1)求水流的横向初始速度vx和纵向初始速度vy;
(2)用含t的代数式表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围);
(3)水流在山坡上的落点C离喷射点A的水平距离是多少米?若要使水流恰好喷射到坡脚B处的小树,在相同仰角下,则需要把喷射点A沿坡面AB方向移动多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③MD=2AM=4EM;④AM=![]() MF.其中正确结论的个数是( )
MF.其中正确结论的个数是( )
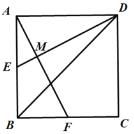
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
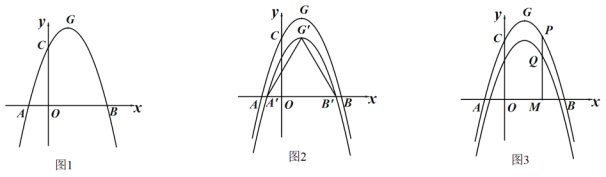
【题目】如图1,抛物线![]() :
:![]() 与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线
与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线![]() 的顶点为G.
的顶点为G.
(1)求出抛物线![]() 的解析式,并写出点G的坐标;
的解析式,并写出点G的坐标;
(2)如图2,将抛物线![]() 向下平移k(k>0)个单位,得到抛物线
向下平移k(k>0)个单位,得到抛物线![]() ,设
,设![]() 与x轴的交点为
与x轴的交点为![]() 、
、![]() ,顶点为
,顶点为![]() ,当△
,当△![]() 是等边三角形时,求k的值:
是等边三角形时,求k的值:
(3)在(2)的条件下,如图3,设点M为x轴正半轴上一动点(介于O与B之间),过点M作x轴的垂线分别交抛物线![]() 、
、![]() 于P、Q两点,是否存在M点,使得以A、Q、M为顶点的三角形与以P、M、B为顶点的三角形相似,若存在,求出点M的坐标:若不存在,请说明理由.
于P、Q两点,是否存在M点,使得以A、Q、M为顶点的三角形与以P、M、B为顶点的三角形相似,若存在,求出点M的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
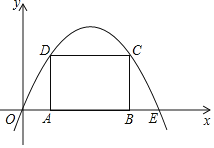
【题目】如图,抛物线y=ax2+bx(a<0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.
(1)求抛物线的函数表达式.
(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?
(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
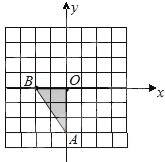
【题目】如图,在平面直角坐标系中,已知△AOB,A(0,﹣3),B(﹣2,0).将△OAB先绕点B 逆时针旋转90°得到△BO1A1,再把所得三角形向上平移2个单位得到△B1A2O2;
(1)在图中画出上述变换的图形,并涂黑;
(2)求△OAB在上述变换过程所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
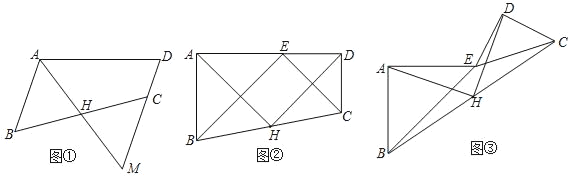
【题目】(1)方法形成
如图①,在四边形ABCD中,AB∥DC,点H是BC的中点,连结AH并延长交DC的延长线于M,则有CM=AB.请说明理由;
(2)方法迁移
如图②,在四边形ABCD中,点H是BC的中点,E是AD上的点,且△ABE和△DEC都是等腰直角三角形,∠BAE=∠EDC=90°.请探究AH与DH之间的关系,并说明理由.
(3)拓展延伸
在(2)的条件下,将Rt△DEC绕点E旋转到图③的位置,请判断(2)中的结论是否依然成立?若成立,请说明理由;若不成立,请举例说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com