
【题目】已知一次函数y=2x﹣4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为d1、d2 . 
(1)当P为线段AB的中点时,求d1+d2的值。
(2)直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标。
(3)若在线段AB上存在无数个P点,使d1+ad2=4(a为常数),求a的值。
【答案】
(1)
解:对于一次函数y=2x﹣4,
令x=0,得到y=﹣4;令y=0,得到x=2,
∴A(2,0),B(0,﹣4),
∵P为AB的中点,
∴P(1,﹣2),
则d1+d2=3
(2)
解:①d1+d2≥2;
②设P(m,2m﹣4),
∴d1+d2=|m|+|2m﹣4|,
当0≤m≤2时,d1+d2=m+4﹣2m=4﹣m=3,
解得:m=1,此时P1(1,﹣2);
当m>2时,d1+d2=m+2m﹣4=3,
解得:m=![]() ,此时P2(
,此时P2(![]() ,
,![]() );
);
当m<0时,不存在,
综上,P的坐标为(1,﹣2)或(![]() ,
,![]() )
)
(3)
解:设P(m,2m﹣4),
∴d1=|2m﹣4|,d2=|m|,
∵P在线段AB上,
∴0≤m≤2,
∴d1=4﹣2m,d2=m,
∵d1+ad2=4,
∴4﹣2m+am=4,即(a﹣2)m=0,
∵有无数个点,
∴a=2.
【解析】(1)对于一次函数解析式,求出A与B的坐标,即可求出P为线段AB的中点时d1+d2的值;
(2)根据题意确定出d1+d2的范围,设P(m,2m﹣4),表示出d1+d2 , 分类讨论m的范围,根据d1+d2=3求出m的值,即可确定出P的坐标;
(3)设P(m,2m﹣4),表示出d1与d2 , 由P在线段上求出m的范围,利用绝对值的代数意义表示出d1与d2 , 代入d1+ad2=4,根据存在无数个点P求出a的值即可.


科目:初中数学 来源: 题型:
【题目】小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.
(1)求小丽步行的速度及学校与公交站台乙之间的距离
(2)当8≤x≤15时,求y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生参加社团的情况,从2010年起,某市教育部门每年都从全市所有学生中随机抽取2000名学生进行调查,图①、图②是部分调查数据的统计图(参加社团的学生每人只能报一项)根据统计图提供的信息解决下列问题:
(1)求图②中“科技类”所在扇形的圆心角α的度数
(2)该市2012年抽取的学生中,参加体育类与理财类社团的学生共有多少人?
(3)该市2014年共有50000名学生,请你估计该市2014年参加社团的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.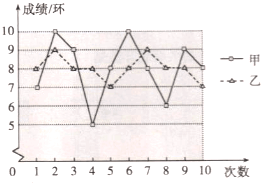
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接写出甲,乙这10次射击成绩的方差s甲2,s乙2哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选 参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,本班应该选 参赛更合适.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(﹣1,m)在直线y=2x+3上,连结OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=﹣x+b上,则b的值为( )
A.-2
B.1
C.![]() ?
?
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和,如:23=3+5,33=7+9+11,43=13+15+17+19,…按此规律,若m3分裂后其中有一个奇数是2015,则m的值是( )
A.46
B.45
C.44
D.43
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com