
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图像与反比例函数![]() 的图像交于A,P两点.
的图像交于A,P两点.
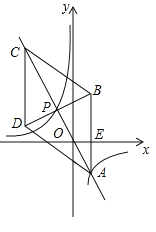
(1)求m,n的值与点A的坐标
(2)求![]() 的值
的值
【答案】(1)m=﹣2,n=1,点A的坐标为(1,﹣2);(2)![]()
【解析】
(1)根据点P的坐标,利用待定系数法可求出m,n的值,联立正、反比例函数解析式成方程组,通过解方程组可求出点A的坐标(利用正、反比例函数图象的对称性结合点P的坐标找出点A的坐标亦可);
(2)由点A的坐标可得出AE,OE,AO的长,由相似三角形的性质可得出∠CDP=∠AOE,再利用正弦的定义即可求出sin∠CDB的值.
(1)解:将点P(-1,2)代入y=mx,得:2=-m,
解得:m=-2,
∴正比例函数解析式为y=-2x;
将点P(-1,2)代入y=![]() ,得:2=-(n-3),
,得:2=-(n-3),
解得:n=1,
∴反比例函数解析式为y=-![]() .
.
联立正、反比例函数解析式成方程组,得: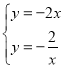 ,
,
解得: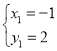 ,
,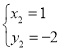 ,
,
∴点A的坐标为(1,-2).
(2)解:∵点A的坐标为(1,-2),
∴AE=2,OE=1,AO=![]() .
.
∵四边形ABCD是菱形,
∴AC⊥BD,AB∥CD,
∴∠DCP=∠BAP,即∠DCP=∠OAE.
∵AB⊥x轴,
∴∠AEO=∠CPD=90°,
∴△CPD∽△AEO,
∴∠CDP=∠AOE,
∴sin∠CDB=sin∠AOE=![]() .
.


 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:
【题目】已知正方形![]() 和正六边形
和正六边形![]() 边长均为1,如图所示,把正方形放置在正六边形外,使
边长均为1,如图所示,把正方形放置在正六边形外,使![]() 边与
边与![]() 边重合,按下列步骤操作:将正方形在正六边形外绕点
边重合,按下列步骤操作:将正方形在正六边形外绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第一次旋转;再绕点
边重合,完成第一次旋转;再绕点![]() 逆时针旋转,使
逆时针旋转,使![]() 边与
边与![]() 边重合,完成第二次旋转;此时点
边重合,完成第二次旋转;此时点![]() 经过路径的长为___________.若按此方式旋转,共完成六次,在这个过程中点
经过路径的长为___________.若按此方式旋转,共完成六次,在这个过程中点![]() ,
,![]() 之间距离的最大值是______.
之间距离的最大值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,漏壶是一种古代计时器.在它内部盛一定量的水,水从壶下的小孔漏出.壶内壁有刻度,人们根据壶中水面的位置计算时间.用x(小时)表示漏水时间,y(厘米)表示壶底到水面的高度,某次计时过程中,记录到部分数据如下表:
漏水时间x(小时) | … | 3 | 4 | 5 | 6 | … |
壶底到水面高度y(厘米) | … | 9 | 7 | 5 | 3 | … |
(1)问y与x的函数关系属于一次函数、二次函数和反比例函数中的哪一种?求出该函数解析式及自变量x的取值范围;
(2)求刚开始计时时壶底到水面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为2,A为圆内一定点,AO=1.P为圆上一动点,以AP为边作等腰△APG,AP=PG,∠APG=120°,OG的最大值为( )

A.1+![]() B.1+2
B.1+2![]() C.2+
C.2+![]() D.2
D.2![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (k>0)与一次函数
(k>0)与一次函数![]() 的图象相交于两点A(
的图象相交于两点A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),线段AB交y轴与C,当|
),线段AB交y轴与C,当|![]() -
-![]() |=2且AC = 2BC时,k、b的值分别为( )
|=2且AC = 2BC时,k、b的值分别为( )

A. k=![]() ,b=2 B. k=
,b=2 B. k=![]() ,b=1 C. k=
,b=1 C. k=![]() ,b=
,b=![]() D. k=
D. k=![]() ,b=
,b=![]()
【答案】D
【解析】∵AC=2BC,∴A点的横坐标的绝对值是B点横坐标绝对值的两倍.∵点A、点B都在一次函数y=x+b的图象上,∴设B(m, ![]() m+b),则A(-2m,-m+b),∵|
m+b),则A(-2m,-m+b),∵|![]() -
-![]() |=2,∴m-(-2m)=2,解得m=
|=2,∴m-(-2m)=2,解得m=![]() ,又∵点A、点B都在反比例函数
,又∵点A、点B都在反比例函数![]() 的图象上,∴
的图象上,∴![]() (
(![]() +b)=(-
+b)=(-![]() )×(-
)×(-![]() +b),解得b=
+b),解得b=![]() ,∴k=
,∴k=![]() ×(
×(![]() +
+![]() )=
)=![]() ,故选D.
,故选D.
【题型】单选题
【结束】
11
【题目】若点(4,m)在反比例函数![]() (x≠0)的图象上,则m的值是 .
(x≠0)的图象上,则m的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点A(x1,1)、B(x2,﹣2)、C(x3,﹣3)在反比例函数y=﹣![]() 的图象上,则x1、x2、x3的大小关系是( )
的图象上,则x1、x2、x3的大小关系是( )
A.x1<x2<x3B.x1<x3<x2C.x3<x1<x2D.x2<x1<x3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列6个结论:①abc<0;②b<a+c; ③4a+2b+c<0;④2a+b+c>0;⑤![]() >0;⑥2a+b=0;其中正确的结论的有_______.
>0;⑥2a+b=0;其中正确的结论的有_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学不仅是一门学科,也是一种文化,即数学文化.数学文化包括数学史、数学美和数学应用等多方面.古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋,为了对聪明的大臣表示感谢,国王答应满足这位大臣的一个要求.大臣说:“就在这个棋盘上放一些米粒吧.第![]() 格放
格放![]() 粒米,第
粒米,第![]() 格放
格放![]() 粒米,第
粒米,第![]() 格放
格放![]() 粒米,然后是
粒米,然后是![]() 粒、
粒、![]() 粒、
粒、![]() 粒······一只到第
粒······一只到第![]() 格.”“你真傻!就要这么一点米粒?”国王哈哈大笑.大臣说:“就怕您的国库里没有这么多米!”国王的国库里真没有这么多米吗?题中问题就是求
格.”“你真傻!就要这么一点米粒?”国王哈哈大笑.大臣说:“就怕您的国库里没有这么多米!”国王的国库里真没有这么多米吗?题中问题就是求![]() 是多少?请同学们阅读以下解答过程就知道答案了.
是多少?请同学们阅读以下解答过程就知道答案了.
设![]() ,
,
则![]()
![]()
![]()
即:![]()
事实上,按照这位大臣的要求,放满一个棋盘上的![]() 个格子需要
个格子需要![]() 粒米.那么
粒米.那么![]() 到底多大呢?借助计算机中的计算器进行计算,可知答案是一个
到底多大呢?借助计算机中的计算器进行计算,可知答案是一个![]() 位数:
位数:![]()
![]() ,这是一个非常大的数,所以国王是不能满足大臣的要求.请用你学到的方法解决以下问题:
,这是一个非常大的数,所以国王是不能满足大臣的要求.请用你学到的方法解决以下问题:
![]() 我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座
我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座![]() 层塔共挂了
层塔共挂了![]() 盏灯,且相邻两层中的下一层灯数是上一层灯数的
盏灯,且相邻两层中的下一层灯数是上一层灯数的![]() 倍,则塔的顶层共有多少盏灯?
倍,则塔的顶层共有多少盏灯?
![]() 计算:
计算: ![]()
![]() 某中学“数学社团”开发了一款应用软件,推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:
某中学“数学社团”开发了一款应用软件,推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:
已知一列数:![]() ,其中第一项是
,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,以此类推,求满足如下条件的所有正整数
,以此类推,求满足如下条件的所有正整数![]() ,且这一数列前
,且这一数列前![]() 项和为
项和为![]() 的正整数幂.请直接写出所有满足条件的软件激活码正整数
的正整数幂.请直接写出所有满足条件的软件激活码正整数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com