
【题目】人们在长期的数学实践中总结了许多解决数学问题的方法,形成了许多光辉的数学想法,其中转化思想是中学教学中最活跃,最实用,也是最重要的数学思想,例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法.
问题提出:求边长分别为、![]() 、
、![]() 、
、![]() 的三角形面积.
的三角形面积.
问题解决:
在解答这个问题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为
![]() 、
、![]() 、
、![]() 的格点三角形
的格点三角形![]() (如图),
(如图),![]() 是角边为1和2的直角三角形斜边,
是角边为1和2的直角三角形斜边,![]() 是直角边分别为1和3的直角三角形的斜边,
是直角边分别为1和3的直角三角形的斜边,![]() 是直角边分别为2和3的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求
是直角边分别为2和3的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求![]() 的高,而借用网格就能计算它的面积.
的高,而借用网格就能计算它的面积.
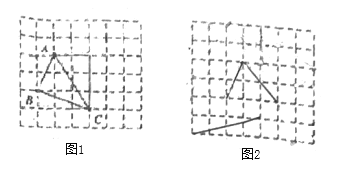
(1)请直接写出图①中![]() 的面积为____________.
的面积为____________.
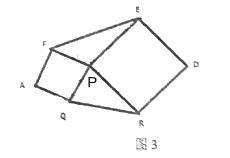
(2)类比迁移:求边长分别为![]() 、
、![]() 、
、![]() 的三角形面积(请利用图②的正方形网格画出相应的
的三角形面积(请利用图②的正方形网格画出相应的![]() ,并求出它的面积)
,并求出它的面积)
(3)思维拓展:求边长分别为![]() ,的三角形的面积
,的三角形的面积
(4)如图(3),已知![]() ,以
,以![]() ,
,![]() 为边向外作正方形
为边向外作正方形![]() ,正方形
,正方形![]() ,连接
,连接![]() ,若
,若![]() ,则六边形
,则六边形 ![]() 的面积是_________.
的面积是_________.
【答案】(1)![]() ;(2)3;(3)5ab;(4)31
;(2)3;(3)5ab;(4)31
【解析】
(1)直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案;
(2)利用勾股定理结合矩形面积减去周围三角形面积进而得出答案;.
(3)结合(1)(2)易得此三角形的三边分别是直角边长为a,4b的直角三角形的斜边;直角边长为3a,2b的直角三角形的斜边;直角边长为2a,2b的直角三角形的斜边.用所在矩形减去周围三角形面积进而得出答案;
(4)将图3的六边形放入网格图中,即可发现其在9×5矩形内,用矩形面积减去周边四个直角三角形和一个梯形面积即可得到答案.
解:(1)S△ABC=3×3-![]() ×1×2-
×1×2-![]() ×1×3-
×1×3-![]() ×2×3=
×2×3=![]() ;
;
故答案为![]()
(2) 如图2所示:△ABC即为所求

![]()
=![]()
=![]()
故答案为3
(3)如图为边长分别为![]() 的三角形,
的三角形,
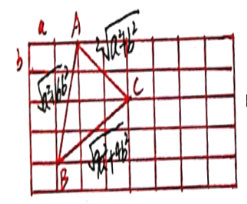
![]()
=![]()
=![]()
(4)如图所示,将六边形放入网格中,可见其在![]() 的矩形内,用矩形面积减去周边四个直角三角形和一个梯形的面积可得六边形的面积
的矩形内,用矩形面积减去周边四个直角三角形和一个梯形的面积可得六边形的面积
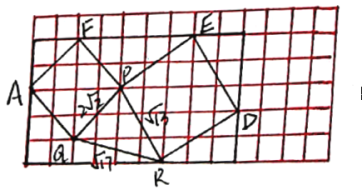
![]()
=![]()
=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
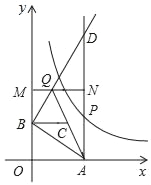
【题目】如图所示,已知:![]() (x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0).动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2
(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0).动点M在y轴上,且在B点上方,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连接AQ,取AQ的中点为C.若四边形BQNC是菱形,面积为2![]() ,此时P点的坐标为( )
,此时P点的坐标为( )
A. (3,2) B. (![]() ,3
,3![]() ) C. (
) C. (![]() ) D. (
) D. (![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
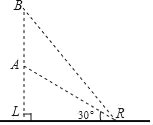
【题目】如图所示,运载火箭从地面L处垂直向上发射,当火箭到达A点时,从位于地面R处的雷达测得AR的距离是40km,仰角是30°,n秒后,火箭到达B点,此时仰角是45°,则火箭在这n秒中上升的高度是_____km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.

(1)如图1,![]() 与
与![]() 的数量关系是__________.
的数量关系是__________.
(2)如图2,若![]() 是线段
是线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,请猜想
,请猜想![]() 三者之间的数量关系,并证明你的结论;
三者之间的数量关系,并证明你的结论;
查看答案和解析>>
科目:初中数学 来源: 题型:
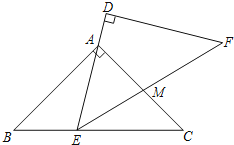
【题目】△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=![]() .现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF运动过程中,若△AEM能构成等腰三角形,则BE的长为______.
.现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF运动过程中,若△AEM能构成等腰三角形,则BE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
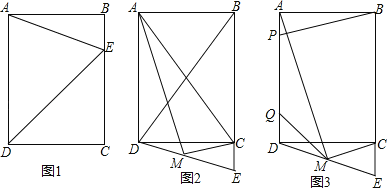
【题目】已知:如图,在矩形ABCD中,AB=6,BC=8,E为直线BC上一点.
(1)如图1,当E在线段BC上,且DE=AD时,求BE的长;
(2)如图2,点E为BC延长长线上一点,若BD=BE,连接DE,M为ED的中点,连接AM,CM,求证:AM⊥CM;
(3)如图3,在(2)条件下,P,Q为AD边上的两个动点,且PQ=5,连接PB、MQ、BM,求四边形PBMQ的周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
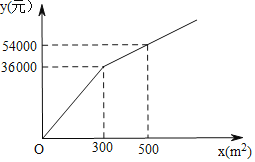
【题目】如图,为了美化环境,建设魅力呼和浩特,呼和浩特市准备在一个广场上种植甲、乙两种花卉经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示乙种花卉的种植费用为每平方米100元
之间的函数关系如图所示乙种花卉的种植费用为每平方米100元
(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式.
的函数关系式.
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com