
����Ŀ����ͼ��Ϊ�����������������������ͺ��أ����ͺ���������һ���㳡����ֲ�ס������ֻ��ܾ��г����飬���ֻ��ܵ���ֲ����![]() ��Ԫ������ֲ���
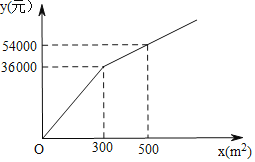
��Ԫ������ֲ���![]() ֮��ĺ�����ϵ��ͼ��ʾ���ֻ��ܵ���ֲ����Ϊÿƽ����100Ԫ
֮��ĺ�����ϵ��ͼ��ʾ���ֻ��ܵ���ֲ����Ϊÿƽ����100Ԫ
��1��ֱ��д����![]() ��
��![]() ʱ��
ʱ��![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2���㳡�ϼס������ֻ��ܵ���ֲ�����![]() �������ֻ��ܵ���ֲ���������
�������ֻ��ܵ���ֲ���������![]() ���Ҳ��������ֻ�����ֲ�����2������ôӦ����������ס������ֻ��ܵ���ֲ�������ʹ��ֲ�ܷ������٣������ܷ���Ϊ����Ԫ��
���Ҳ��������ֻ�����ֲ�����2������ôӦ����������ס������ֻ��ܵ���ֲ�������ʹ��ֲ�ܷ������٣������ܷ���Ϊ����Ԫ��
���𰸡���1��![]() ����2��Ӧ�÷���ס������ֻ��ܵ���ֲ����ֱ���800m2��400m2������ʹ��ֲ�ܷ������٣������ܷ���Ϊ121000Ԫ��
����2��Ӧ�÷���ס������ֻ��ܵ���ֲ����ֱ���800m2��400m2������ʹ��ֲ�ܷ������٣������ܷ���Ϊ121000Ԫ��
��������
��1����ͼ��֪y��x�ĺ�����ϵʽ�Ƿֶκ���������ϵ���������ʽ���ɣ�
��2������ֲ�ܷ���ΪWԪ�����ֻ�����ֲΪam2�������ֻ�����ֲ��1200a��m2������ʵ���������ȷ��a�ķ�Χ�������ֲ����y��Ԫ������ֲ���x��m2��֮��ĺ�����ϵ���Է����������ٷ���Ϊ���٣�
�⣺��1����0��x��300����y=kx�����㣨300,36000������ã�
36000=300k��
��k=120��
��x��300����y=mx+n�����㣨300,36000�����㣨500,54000������
��![]() �����m=90��n=9000��
�����m=90��n=9000��
��y=90x+9000��
��![]() ��
��
��2������ֲ�ܷ���ΪWԪ�����ֻ�����ֲΪam2�������ֻ�����ֲ��1200a��m2��
������ã�![]() ��
��
��200��a��800
��200��a��300ʱ��W1��120a��100��1200a����20a��120000��
��20��0��W1��a���������
�൱a��200ʱ��Wmin��124000Ԫ
��300��a��800ʱ��W2��90a��9000��100��1200a����10a +129000��
��-10��0��W2��a���������
��a��800ʱ��Wmin��121000Ԫ
��124000��121000
�൱a��800ʱ���ܷ������٣������ܷ���Ϊ121000Ԫ��
��ʱ���ֻ�����ֲ���Ϊ1200800��400��m2����
��Ӧ�÷���ס������ֻ��ܵ���ֲ����ֱ���800m2��400m2������ʹ��ֲ�ܷ������٣������ܷ���Ϊ121000Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڳ��ڵ���ѧʵ�����ܽ�����������ѧ����ķ������γ��������Ե���ѧ�뷨������ת��˼������ѧ��ѧ�����Ծ����ʵ�ã�Ҳ������Ҫ����ѧ˼�룬���罫������ͼ��ת��Ϊ����ͼ�ξ����о�ͼ������Ƚϳ��õ�һ�ַ�����
�����������߳��ֱ�Ϊ��![]() ��
��![]() ��
��![]() �������������
�������������
��������
�ڽ���������ʱ���Ƚ���һ������������ÿ��С�����εı߳�Ϊ1�������������л����߳��ֱ�Ϊ
![]() ��
��![]() ��
��![]() �ĸ��������
�ĸ��������![]() ����ͼ����
����ͼ����![]() �ǽDZ�Ϊ1��2��ֱ��������б�ߣ�
�ǽDZ�Ϊ1��2��ֱ��������б�ߣ�![]() ��ֱ�DZ߷ֱ�Ϊ1��3��ֱ�������ε�б�ߣ�
��ֱ�DZ߷ֱ�Ϊ1��3��ֱ�������ε�б�ߣ�![]() ��ֱ�DZ߷ֱ�Ϊ2��3��ֱ��������б�ߣ���һ�����ε������ȥ����ֱ�������ε����������������
��ֱ�DZ߷ֱ�Ϊ2��3��ֱ��������б�ߣ���һ�����ε������ȥ����ֱ�������ε����������������![]() �ĸߣ�������������ܼ����������.
�ĸߣ�������������ܼ����������.
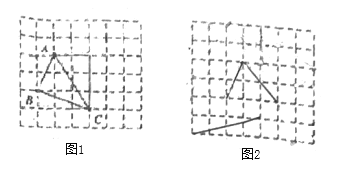
��1����ֱ��д��ͼ����![]() �����Ϊ____________.
�����Ϊ____________.
��2�����Ǩ�ƣ���߳��ֱ�Ϊ![]() ��
��![]() ��
��![]() �������������������ͼ�ڵ�������������Ӧ��
�������������������ͼ�ڵ�������������Ӧ��![]() ����������������
����������������
��3��˼ά��չ����߳��ֱ�Ϊ![]() ���������ε����
������������
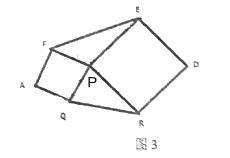
��4����ͼ��3������֪![]() ����
����![]() ��
��![]() ��������������
��������������![]() ��������
��������![]() ������
������![]() ����
����![]() ����������
���������� ![]() �������_________.
�������_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
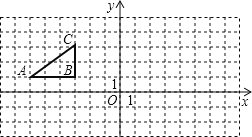
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ�Rt��ABC�Ķ�����ڸ���ϣ��ڽ���ƽ��ֱ������ϵ��A������Ϊ��-6��1������B������Ϊ��-3��1������C������Ϊ��-3��3����
��1����ԭ����Rt��ABC�Ƶ�O˳ʱ����ת90���õ�Rt��A1B1C1������ͼ�ϻ���Rt��A1B1C1��ͼ�Σ�
��2�����߶�BCɨ���������
��3�����A��ת��A1·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB=AC����A=60������D���߶�BC���е㣬��EDF=120�㣬DE���߶�AB�ཻ�ڵ�E��DF���߶�AC����AC���ӳ��ߣ��ཻ�ڵ�F��
��1����ͼ����DF��AC������ΪF��֤����DE=DF
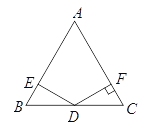
��2����ͼ������1���е���EDF�Ƶ�D˳ʱ����תһ���ĽǶȣ�DF�����߶�AC�ཻ�ڵ�F��DE=DF��Ȼ������˵�����ɡ�
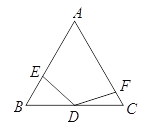
��3������EDF�����Ƶ�D˳ʱ����תһ���ĽǶȣ�ʹDF���߶�AC���ӳ����ཻ�ڵ�F��DE=DF��Ȼ������ ֱ��˵�����ۣ�����˵�����ɡ�
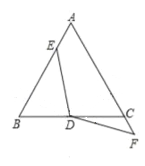
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���![]() �������Σ�
�������Σ�![]() ��ֱ��
��ֱ��![]() ������һ�㣬
������һ�㣬![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() .����G��BC����ʱ����ͼ1������֤DF-BE=EF.
.����G��BC����ʱ����ͼ1������֤DF-BE=EF.
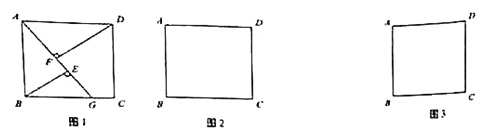
��1������![]() ��
��![]() �ӳ�����ʱ����ͼ2�в�ȫͼ�Σ�д��
�ӳ�����ʱ����ͼ2�в�ȫͼ�Σ�д��![]() ��
��![]() ��
��![]() ��������ϵ����֤����
��������ϵ����֤����
��2������![]() ��
��![]() �ӳ�����ʱ����ͼ3�в�ȫͼ�Σ�д��
�ӳ�����ʱ����ͼ3�в�ȫͼ�Σ�д��![]() ��
��![]() ��
��![]() ��������ϵ������֤��.
��������ϵ������֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+c��x���һ������A������Ϊ����1��0�����Գ���Ϊֱ��x=��2��
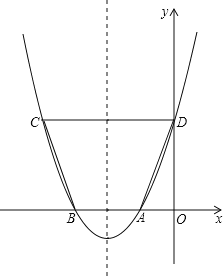
��1������������x�����һ������B�����ꣻ
��2����D����������y��Ľ��㣬��C���������ϵ���һ�㣮��֪��ABΪһ�ױߵ�����ABCD�����Ϊ9����������ߵĽ���ʽ����ָ������E�����ꣻ
��3����P�ǣ�2���������߶Գ�����һ���㣬����1����λ/����ٶȴӴ������ߵĶ���E�����˶������P�˶���ʱ��Ϊt�룮
����tΪ�� ����ʱ����PAD���ܳ���С����tΪ�� ����ʱ����PAD����ADΪ���ĵ��������Σ�������������ţ�
����P���˶������У��Ƿ����һ��P��ʹ��PAD����ADΪб�ߵ�ֱ�������Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ũ��ʦʯ������ij��ѧ������1�����ѧ������һ����ѧ����У������������㳡�����������ڹ㳡���ĵ�������ͭ��߶ȣ���֪ͭ������ĸ�Ϊ3.5m��ijС���ʵϰ������������������ͭ��ĸߣ������ȷ��0.1m��
ʵϰ����2003��9��25��
��Ŀ1 | �����ײ����Ե����ͭ��� | |||
| ||||
�� �� �� �� | ������Ŀ | ��һ�� | �ڶ��� | ƽ��ֵ |
BD�ij� | 12.3m | 11.7m | ||
������CD�ĸ� | 1.32m | 1.28m | ||
��� | ��=30��56' | ��=31��4' | ||
�� �� | ||||
��� | ||||
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϲ��ش����⣮����֪����![]() ��
��![]() ����������������ж��θ�ʽ�ķ������ʽ��ˣ����ǵĻ��������θ�ʽ����˵�������������ʽ��Ϊ��������ʽ����
����������������ж��θ�ʽ�ķ������ʽ��ˣ����ǵĻ��������θ�ʽ����˵�������������ʽ��Ϊ��������ʽ����![]() ��
��![]() ��Ϊ��������ʽ��
��Ϊ��������ʽ��![]() ��
��![]() ��Ϊ��������ʽ�����ݻ�Ϊ��������ʽ�Ļ��������������Խ���ĸ�к��ж��θ�ʽ�Ĵ���ʽ��Ϊ��ĸ���������Ĵ���ʽ��������̳�Ϊ��ĸ�����������磺
��Ϊ��������ʽ�����ݻ�Ϊ��������ʽ�Ļ��������������Խ���ĸ�к��ж��θ�ʽ�Ĵ���ʽ��Ϊ��ĸ���������Ĵ���ʽ��������̳�Ϊ��ĸ�����������磺![]() �������������⣺
�������������⣺
��1��![]() ��ĸ�������Ľ���� ��
��ĸ�������Ľ���� ��![]() ��ĸ�������Ľ���� ��
��ĸ�������Ľ���� ��
��2�����㣺![]() ��
��
��3����ʵ��![]() ��
��![]() ���ж�
���ж�![]() ��
��![]() �Ĵ�С����˵�����ɣ�
�Ĵ�С����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
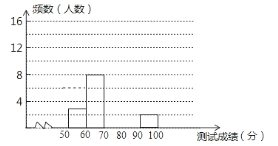
����Ŀ��Ϊ����ǿѧ��������ʶ�������ٰ�����������֪ʶ����������ѡ�κ���30��ѧ���μӾ�������30����ѧ��ͬ�½��50��ѡ���⣬��ÿ��ȷһ��ѡ�����2�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 50��x��60 | 3 |
��2�� | 60��x��70 | 8 |
��3�� | 70��x��80 | 13 |
��4�� | 80��x��90 | a |
��5�� | 90��x��100 | 2 |
��1�������a��ֵ��
��2�����Ƶ���ֲ�ֱ��ͼ����������
��3�������Գɼ�������80��Ϊ���㣬�β��Ե��������Ƕ��٣�
��4����4���ͬѧ�����3���Ե�һ��3��ͬѧ������һ��һ�����������4���С����Сǿ��ͬʱ�鵽�ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com