
����Ŀ���Ķ����в��ϲ��ش����⣮����֪����![]() ��
��![]() ����������������ж��θ�ʽ�ķ������ʽ��ˣ����ǵĻ��������θ�ʽ����˵�������������ʽ��Ϊ��������ʽ����
����������������ж��θ�ʽ�ķ������ʽ��ˣ����ǵĻ��������θ�ʽ����˵�������������ʽ��Ϊ��������ʽ����![]() ��
��![]() ��Ϊ��������ʽ��
��Ϊ��������ʽ��![]() ��
��![]() ��Ϊ��������ʽ�����ݻ�Ϊ��������ʽ�Ļ��������������Խ���ĸ�к��ж��θ�ʽ�Ĵ���ʽ��Ϊ��ĸ���������Ĵ���ʽ��������̳�Ϊ��ĸ�����������磺
��Ϊ��������ʽ�����ݻ�Ϊ��������ʽ�Ļ��������������Խ���ĸ�к��ж��θ�ʽ�Ĵ���ʽ��Ϊ��ĸ���������Ĵ���ʽ��������̳�Ϊ��ĸ�����������磺![]() �������������⣺
�������������⣺
��1��![]() ��ĸ�������Ľ���� ��
��ĸ�������Ľ���� ��![]() ��ĸ�������Ľ���� ��
��ĸ�������Ľ���� ��
��2�����㣺![]() ��
��
��3����ʵ��![]() ��
��![]() ���ж�
���ж�![]() ��
��![]() �Ĵ�С����˵�����ɣ�
�Ĵ�С����˵�����ɣ�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
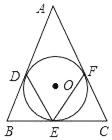
����Ŀ����ͼ����ABC�����߷ֱ��С�O��D��E��F��
��1������A��40�������DEF�Ķ�����
��2��AB��AC��13��BC��10�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
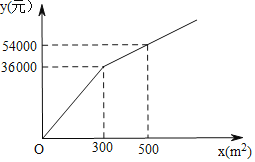
����Ŀ����ͼ��Ϊ�����������������������ͺ��أ����ͺ���������һ���㳡����ֲ�ס������ֻ��ܾ��г����飬���ֻ��ܵ���ֲ����![]() ��Ԫ������ֲ���
��Ԫ������ֲ���![]() ֮��ĺ�����ϵ��ͼ��ʾ���ֻ��ܵ���ֲ����Ϊÿƽ����100Ԫ
֮��ĺ�����ϵ��ͼ��ʾ���ֻ��ܵ���ֲ����Ϊÿƽ����100Ԫ
��1��ֱ��д����![]() ��
��![]() ʱ��
ʱ��![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2���㳡�ϼס������ֻ��ܵ���ֲ�����![]() �������ֻ��ܵ���ֲ���������
�������ֻ��ܵ���ֲ���������![]() ���Ҳ��������ֻ�����ֲ�����2������ôӦ����������ס������ֻ��ܵ���ֲ�������ʹ��ֲ�ܷ������٣������ܷ���Ϊ����Ԫ��
���Ҳ��������ֻ�����ֲ�����2������ôӦ����������ס������ֻ��ܵ���ֲ�������ʹ��ֲ�ܷ������٣������ܷ���Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��E��F ��ƽ���ı��� ABCD �ĶԽ��� AC �ϵ����㣬AE=CF��

��֤����1��EB DF ��
��2��EB��DF ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD �У��Ե� A ΪԲ�ģ�AB ��Ϊ�뾶������ AD �ڵ� F���ٷֱ��Ե� B��F ΪԲ�ģ�����![]() BF ����ͬ��Ϊ�뾶�������������ڵ� P������ AP ���ӳ��� BC �ڵ� E������ EF��
BF ����ͬ��Ϊ�뾶�������������ڵ� P������ AP ���ӳ��� BC �ڵ� E������ EF��
��1���������ϳ߹���ͼ�Ĺ��̣�֤���ı��� ABEF �����Σ�
��2�������� ABEF �ı߳�Ϊ 2��AE�� 2 ![]() �������� ABEF �������
�������� ABEF �������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һˮ�ص��ݻ�V����������ע��ˮ��ʱ��t�����ӣ�֮�俪ʼ��һ�κ�����ϵ�����м�¼�������ʱ��ע��ˮ��ʱ����ˮ���ݻ����ֶ�Ӧֵ��
ע��ˮ��ʱ��t�����ӣ� | 0 | 10 | �� | 25 |
ˮ�ص��ݻ�V�������� | 100 | 300 | �� | 600 |
��1�������ʱ��ʱV����t�ĺ�����ϵʽ������Ҫд�������Ķ�����
��2����tΪ25���ӿ�ʼ��ÿ����ע���ˮ�������仯�ˣ���tΪ27����ʱ��ˮ�ص��ݻ�Ϊ726������������������е�ÿ����ע���ˮ�������İٷ�����ͬ��������ٷ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
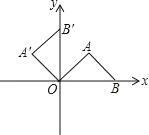
����Ŀ����ֱ������ϵ�У�����ֱ��������AOB����ͼ��ʾ��λ�ã���B�ĺ�����Ϊ2������AOB�Ƶ�O����ʱ�뷽����ת90�㣬�õ���A��OB�䣬���A�������Ϊ��������
A. ��1��1�� B. ��![]() ��
��![]() ��
��
C. ����1��1�� D. ����![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
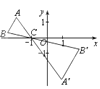
����Ŀ����ͼ����ABC�У�A��B����������x����Ϸ�����C��������(-1��0)���Ե�CΪλ�����ģ���x����·�����ABC��λ��ͼ�Σ����ѡ�ABC�ı߳��Ŵ�ԭ����2���������õ����ǡ�A��B��C�����B�Ķ�Ӧ��B���ĺ�������a�����B�ĺ��������� ��
A. -![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȫ�ȵĺ�30��ǵ�ֱ�����ǰ��ص���һ����ͼ������A��B��C����AC���е�Mת����б��A��B��պù���ABC��ֱ�Ƕ���C��������ABC��б��AB���ڵ�N������AA�䡢C��C��AC�䣮��AC�ij�Ϊ2��������������ۣ���AA��=1����C��C��A��B�䣻����N�DZ�AB���е㣻���ı���AA��CC��Ϊ���Σ���A��N=B��C=![]() ��������ȷ���У�������
��������ȷ���У�������
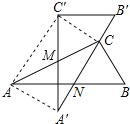
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com